Inner product

The following three things are basic in the vector of space. (1) Sum, (2) Scalar multiplication, (3) Inner product (scalar product)

Now that we have already learned about sums and scalar multiplication, we will introduce the inner product of vectors in space.

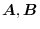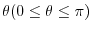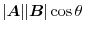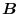Let the non-zero vectors $\boldsymbol{A}, \boldsymbol{B}$ and their angles be $\theta (0 \leq \theta \leq \pi)$ . Then the real number $\vert\boldsymbol{A}\vert\vert\boldsymbol{B}\vert\cos{\theta}$ is called inner product or scalar product of $\boldsymbol{A}$ and $\boldsymbol{B}$ and denoted by 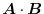$\boldsymbol{A} \cdot\boldsymbol{B}$ . Thus,

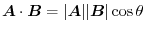
$\displaystyle \boldsymbol{A} \cdot\boldsymbol{B} = \vert\boldsymbol{A}\vert\vert\boldsymbol{B}\vert\cos{\theta}$

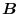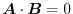If at least one of $\boldsymbol{A}$ and $\boldsymbol{B}$ is bf 0, set $\boldsymbol{A} \cdot \boldsymbol{B} = 0$ .

Theorem 1..1

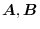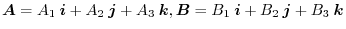For two vectors $\boldsymbol{A}, \boldsymbol{B}$ ，if $\boldsymbol{A} = A_{1}\:\boldsymbol{i} + A_{2}\:\boldsymbol{j} + A_{3}\:\boldsy... ...mbol{B} = B_{1}\:\boldsymbol{i} + B_{2}\:\boldsymbol{j} + B_{3}\:\boldsymbol{k}$ ，then

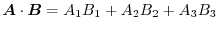
$\displaystyle \boldsymbol{A} \cdot\boldsymbol{B} = A_{1}B_{1} + A_{2}B_{2} + A_{3}B_{3}$

．

Question 1..2

Prove the above theorem using the definition of inner product and the law of cosines.．

Example 1..2

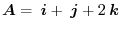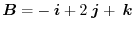Find the angle between $\boldsymbol{A} = \:\boldsymbol{i} + \:\boldsymbol{j} + 2\:\boldsymbol{k}$ and $\boldsymbol{B} = -\:\boldsymbol{i} + 2\:\boldsymbol{j} + \:\boldsymbol{k}$ . Abswer

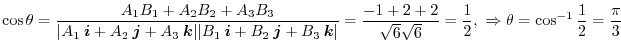
$\displaystyle \cos{\theta} = \frac{A_{1}B_{1} + A_{2}B_{2} + A_{3}B_{3}}{\vert ... ...}} = \frac{1}{2},\ \Rightarrow \theta = \cos^{-1}{\frac{1}{2}} = \frac{\pi}{3}$

Question 1..3

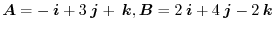For $\boldsymbol{A} = -\:\boldsymbol{i} + 3\:\boldsymbol{j} + \:\boldsymbol{k}, \boldsymbol{B} = 2\:\boldsymbol{i} + 4\:\boldsymbol{j} - 2\:\boldsymbol{k}$ , find the following values:

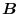(1) Angle between $\boldsymbol{A}$ and $\boldsymbol{B}$ (2) A unit vector with the direction of $\boldsymbol{A}$