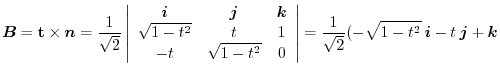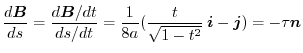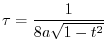Next: Scalar field, vector field Up: Differentiation / integration of Previous: Space curves Contents Index
The curve
![$\displaystyle C : \boldsymbol{r}(t) = (x(t), y(t), z(t)), \ t \in [a,b] $](img278.png)
![$[a, b]$](img126.png) is considered as the interval of time, and
is considered as the interval of time, and
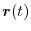 is considered as the position of the object in time
is considered as the position of the object in time 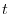 .
For the motion
.
For the motion
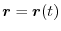 ,
,
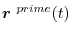 is called velocity.Also,
is called velocity.Also,
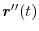 is acceleration and expressed by
is acceleration and expressed by
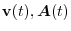 .
Thus,,
.
Thus,,
|
As we have already learned, the tangent unit vector can be represented by
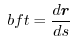 and the velocity vector is
and the velocity vector is
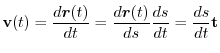
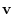 ,
,
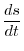 is the rate or speed of change in arc length and denoted by
is the rate or speed of change in arc length and denoted by 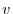 . Thus
. Thus
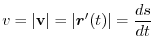
Next, to understand the acceleration a little better, let's consider the velocity vector.
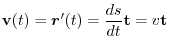
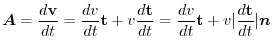
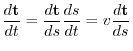
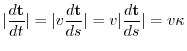
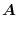 |
 |
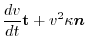 |
|
 |
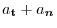 |
|
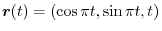
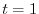 , find
, find
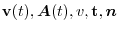 .
.
Answer
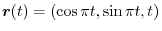
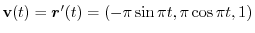
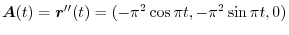
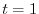 ,
,
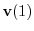 |
 |
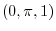 |
|
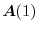 |
 |
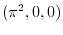 |
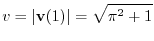
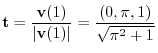
 .
Here we will consider a method that is easy to calculate.
.
Here we will consider a method that is easy to calculate.
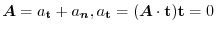
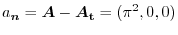
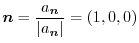
Other way is
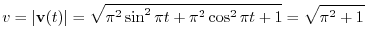
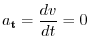
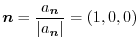
The vector
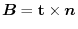
 and the normal vector
and the normal vector
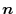 is called binormal unit vector. Also, the
is called binormal unit vector. Also, the 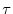 satisfying
satisfying
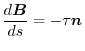
Now, let's examine the three unit vectors
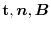 that have appeared so far.
that have appeared so far.
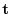 and
and
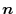 is called osculating plane. the plane made by
is called osculating plane. the plane made by
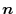 and
and
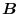 is called normal plane. the plane made by
is called normal plane. the plane made by 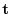 and
and
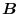 is called rectifying plane.
is called rectifying plane.
First,
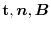 are orthogonal to each other. Also, these vectors satisfies the following relations.
are orthogonal to each other. Also, these vectors satisfies the following relations.
|
Proof
By the equation 2.1,
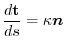 . Also, by the definition of torsion,
. Also, by the definition of torsion,
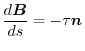 .Next differentiate
.Next differentiate
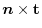 with respect to
with respect to  , we have
, we have
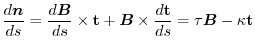
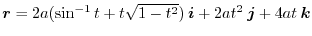 ,find the followings. However,
,find the followings. However, 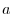 is an arbitrary positive constant.
is an arbitrary positive constant.
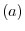 the arc length the curve for
the arc length the curve for
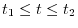
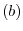 the unit tangent vector
the unit tangent vector 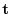
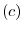 the normal vector
the normal vector
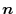 and the curvature
and the curvature 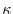
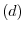 the binormal vector
the binormal vector
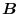 and the torsion
and the torsion 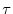
Answer
(a)
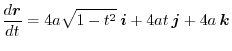 implies
implies
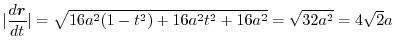
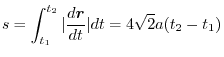
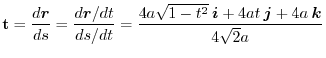
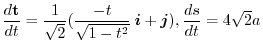 より
より
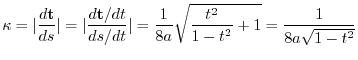
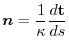 より
より
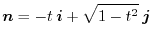
(d)