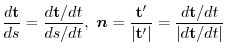Next: Motion of objects Up: Differentiation / integration of Previous: Differentiation / integration of Contents Index
The space curve (hodograph) drawn by the point P  in space is given by
in space is given by
![$\displaystyle C = \{(x,y,z): x = x(t), y = y(t), z = z(t), t \in [a, b] \} $](img184.png)
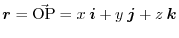 , and given as a vector function of
, and given as a vector function of 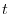
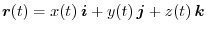
Next, let's think about what the derivative
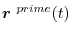 of the vector function
of the vector function
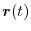 represents geometrically.
The derivative of a vector function
represents geometrically.
The derivative of a vector function
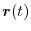 ,
,
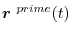 is by the definition
is by the definition
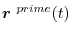 .
.
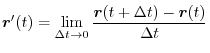
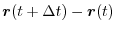 is
is
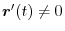 ,then even if
,then even if 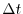 approaches 0 , it not
approaches 0 , it not 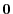 and it approaches the direction of the tangent vector,Thus, the limit
and it approaches the direction of the tangent vector,Thus, the limit
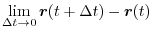
Unfortunately, this limit cannot be used as a tangent direction vector. Because this limit is 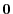 and
and 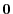 has no direction.
has no direction.
Therefore, to avoid this, consider the following vector that can obtain a large length when 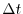 is small.
is small.
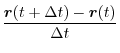
This vector is parallel to
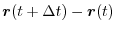 when
when 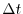 is non-zero.That is, this vector is parallel to the tangent direction vector. Therefore, when this limit value
is non-zero.That is, this vector is parallel to the tangent direction vector. Therefore, when this limit value
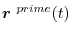 exists, this limit value can be considered as a tangent direction vector, so
exists, this limit value can be considered as a tangent direction vector, so
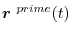 is called tangent vector of curve
is called tangent vector of curve
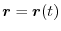 .
Also,
.
Also,
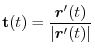
Note that
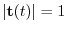 here, from the example 2
here, from the example 2
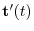 and
and
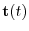 is orthogonal.So,
is orthogonal.So,
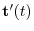 is called normal vector
is called normal vector
 . Also, for
. Also, for
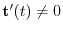 ,
,
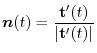
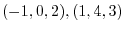 .
.
Answer
The straight line to be found has a starting point of 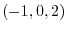 and a direction of
and a direction of
![${}^t [1,4,3]-{}^t [-1,0,2] = {}^t [2,4,1]$](img208.png) . Let the arbitrary point on the line as
. Let the arbitrary point on the line as 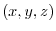 . Then,
. Then,
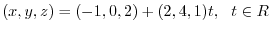
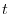 , we have
, we have
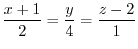
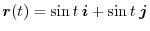 .
.
Answer
Since
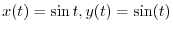 , we have
, we have 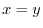 .t should be noted here that the value of
.t should be noted here that the value of 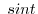 is from
is from 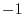 to
to 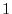 , so the curve to be calculated is
, so the curve to be calculated is
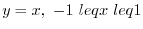 .
.
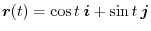 at
at
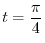 .
.
Answer The tangent vector is give by
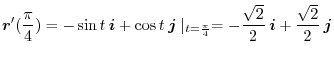
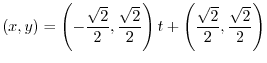
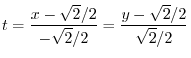
When
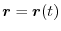 satisfies the condition
satisfies the condition
![$\boldsymbol{r}^{\prime}(t) \neq 0, \boldsymbol{r}^{\prime}(t) \in C[a,b]$](img223.png) ,we say
,we say
 is smooth curve.The length of the
is smooth curve.The length of the
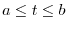 part of a smooth curve
part of a smooth curve
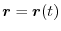 is called arc length an denoted by
is called arc length an denoted by 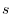 .
How can you find the arc length?
.
How can you find the arc length?
Curve
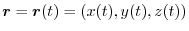 corresponding to the small interval
corresponding to the small interval
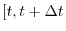 in the interval
in the interval ![$[a, b]$](img126.png) . The length of the arc PQ is considered to be approximated by the line segment PQ. Then
. The length of the arc PQ is considered to be approximated by the line segment PQ. Then
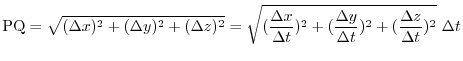
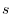 is expressed by
is expressed by
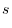 |
 |
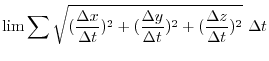 |
|
 |
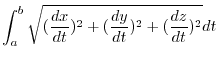 |
||
 |
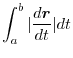 |
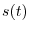 from
from
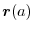 to
to
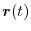 is given by
is given by
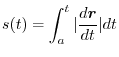
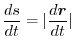
|
As you may have noticed here, if you think of 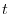 as time, then
as time, then
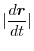 is considered to be a change in position within a minute time. Therefore, it represents the moving speed of the point P. Therefore, the length
is considered to be a change in position within a minute time. Therefore, it represents the moving speed of the point P. Therefore, the length 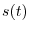 of the curve can be thought of as the distance that the point P has moved within the time
of the curve can be thought of as the distance that the point P has moved within the time 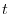 .
.
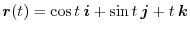 for
for
 .
.
Answer
Since
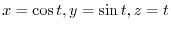 ,we have
,we have
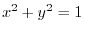 . Thus,
. Thus,
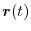 is a smooth curve that spirally rotates around a cylinder with a radius of 1.
is a smooth curve that spirally rotates around a cylinder with a radius of 1.
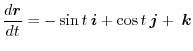
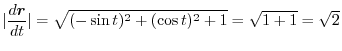
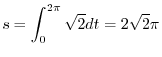
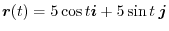 using the arc length
using the arc length 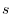 as a parameter.
as a parameter.
Answer
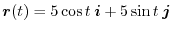 implies
implies
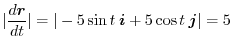
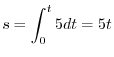
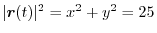 implies
implies
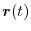 is a circle of the radius 5 with the center at the origin. Thus, the arc length is
is a circle of the radius 5 with the center at the origin. Thus, the arc length is 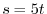 .Therefore,
.Therefore,
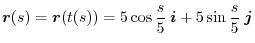
When the curve  is expressed by
is expressed by
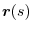 using the parameter
using the parameter  ,we find the tangent vector.
,we find the tangent vector.
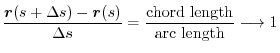
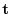 is expressed by
is expressed by
|
Now let's think about how the curve bends. First, let's think about the curve on the plane.Let  be the angle formed by the tangent
be the angle formed by the tangent 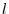 and the
and the 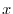 axis at the point P on the curve. The tangents
axis at the point P on the curve. The tangents 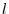 and
and  change as the point P moves.At this time, the rate of change of
change as the point P moves.At this time, the rate of change of  per unit arc length is called curvature(curvature) .
per unit arc length is called curvature(curvature) .
|
Where the tangent unit vector 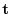 can be represented by
can be represented by
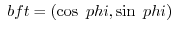 .Therefore, when examining the rate of change of the tangent vector per unit arc length,
.Therefore, when examining the rate of change of the tangent vector per unit arc length,
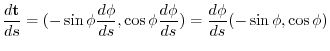
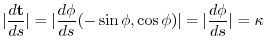
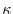 can also be expressed by the rate of change of the tangent vector per unit arc length.
can also be expressed by the rate of change of the tangent vector per unit arc length.
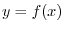 .
.
Answer
First find
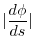 .
.
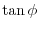 is the slope of the tangent line. Thus
is the slope of the tangent line. Thus
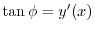 Therefore,
Therefore,
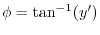
 .
.
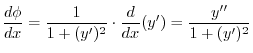
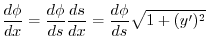
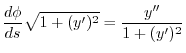
|
The curvature of the curve in space is
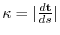 .
.