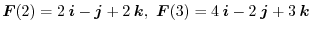Space curve

Exercise2.1

1.

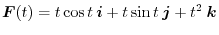For $${\boldsymbol{F}(t) = t\cos{t} \:\boldsymbol{i} + t\sin{t} \:\boldsymbol{j} + t^2 \:\boldsymbol{k}}$$，find the trace of $\boldsymbol{F}(t)$ .

2.

For $${\boldsymbol{F}(t) = t^{2}\:\boldsymbol{i} + t\:\boldsymbol{j} + t^{3}\:\boldsymbol{k}}$$， find $\boldsymbol{F}^{\prime}(t)$.

3.

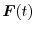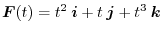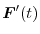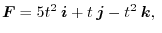
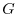
For $\boldsymbol{F} = 5t^2\:\boldsymbol{i} + t\:\boldsymbol{j} - t^2\:\boldsymbol{k}, \$   $G$$= \sin{t}\:\boldsymbol{i} - \cos{t}\:\boldsymbol{j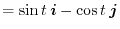}$，find the followings:

(1)

$(\boldsymbol{F}\cdot$$G$$)'$

(2)

$(\boldsymbol{F} \times$   $G$$)'$

4.

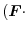
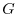
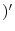
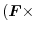
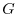
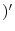
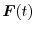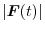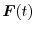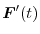Suppose that the magnitude of $\boldsymbol{F}(t)$, $\vert\boldsymbol{F}(t)\vert$ is constant，show that $\boldsymbol{F}(t)$ and $\boldsymbol{F}^{\prime}(t)$ are orthogonal for all $t$．

5.

For every vector function $\boldsymbol{F} = \boldsymbol{F}(t)$，prove that $\int \boldsymbol{F}\cdot\boldsymbol{F}'\;dt = \frac{1}{2}\boldsymbol{F}\cdot\boldsymbol{F}$.

6.

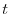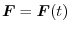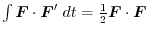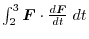Evaluate $\int_{2}^{3}\boldsymbol{F}\cdot\frac{d\boldsymbol{F}}{dt}\;dt$, provided $\boldsymbol{F}(2) = 2\:\boldsymbol{i} -\boldsymbol{j} + 2\:\boldsymbol{k},\ \boldsymbol{F}(3) = 4\:\boldsymbol{i} - 2\:\boldsymbol{j} + 3\:\boldsymbol{k}$