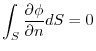Next: Stokes'theorem Up: Integral formula Previous: Integral formula Contents Index
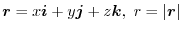 .Prove that for any region
.Prove that for any region 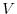 and the boundary surface
and the boundary surface  , the followings are true.
, the followings are true.
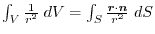
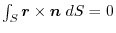
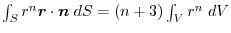
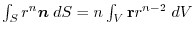
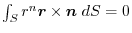
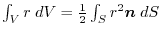
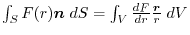
 of any region
of any region 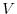 in the scalar field
in the scalar field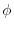 .
.
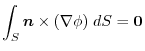
 satisfies
satisfies
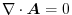 .Take the closed curve
.Take the closed curve 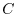 that is the boundary of the curved surface
that is the boundary of the curved surface  in this vector field.At this time, the surface integral
in this vector field.At this time, the surface integral
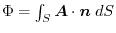 is always the same value for any curved surface
is always the same value for any curved surface  whose boundary is
whose boundary is 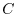 . And its value is determined by the closed surface
. And its value is determined by the closed surface 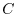 .Prove the above.
.Prove the above.
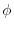 and the vector field
and the vector field
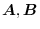 are within the comon domain. Prove the following equation for any region
are within the comon domain. Prove the following equation for any region 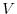 and its bounary surface
and its bounary surface  .
.
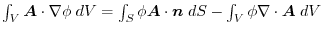
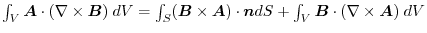
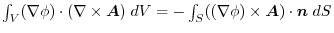
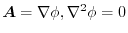 ならば,
ならば,
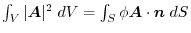
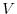 and its boundary surface
and its boundary surface  within the common definition of the scalar fields
within the common definition of the scalar fields 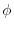 and
and 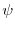 .
.
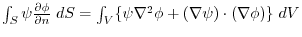
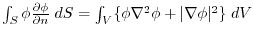
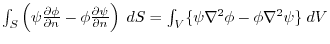 Green's formula
Green's formula
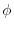 is harmonic function, then
is harmonic function, then
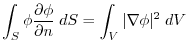
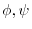 are harmonic functions, then
are harmonic functions, then
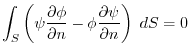
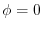 on
on  ,then the harmonic function
,then the harmonic function 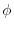 is 0 in
is 0 in 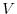 .
.
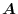 is defined in all space. Prove that if
is defined in all space. Prove that if
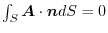 for any boundary surface
for any boundary surface  ,then
,then
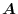 has a vector potential.
has a vector potential.
 is defined for all space. Prove that if
is defined for all space. Prove that if
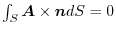 for any boundary surface
for any boundary surface  ,then
,then
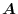 has a scalar potential.
has a scalar potential.
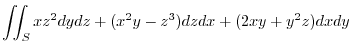
 is the upper sphere
is the upper sphere
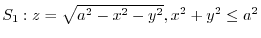 と
と
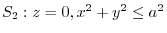 .
.
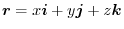 .Show the followings for the region
.Show the followings for the region 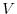 and the boundary surface
and the boundary surface  . Here, denote the vaolume of the region
. Here, denote the vaolume of the region  by
by 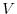 .
.
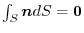
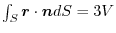
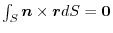
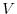 in the scalar field
in the scalar field 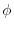 and its boundary surface
and its boundary surface  .
.
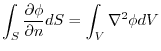
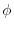 is a harmonic function, then
is a harmonic function, then