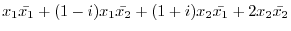Normal Matrix

Exercise4-4

1. Find the unitary matrix 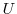$U$ so that 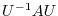$U^{-1}AU$ is diagonal.

$$A = \left(\begin{array}{cc} 1&1-i\\ 1+i&2 \end{array}\right)$$

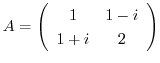
2. Find the orthogonal matrix 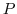$P$ so that 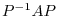$P^{-1}AP$ is diagonal.

$$A = \left(\begin{array}{rrr} 1&0&-1\\ 0&-1&0\\ -1&0&1 \end{array}\right)$$

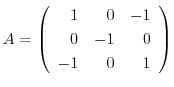
3. Find a condition so that 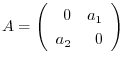$A = \left(\begin{array}{rr} 0&a_{1}\\ a_{2}&0 \end{array}\right)$ can be transformed to diagonal matrix by the unitary matrix．

4. Find the orthogonal matrix so that the following bilinear form becomes the standard form.

$$x_{1}^2 + 2x_{2}^{2} - 3x_{3}^{2} + 2x_{1}x_{2}$$

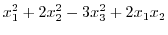
5. Standarize the following Hermite matrix by using unitary matrix.

$$x_{1}\bar{x_{1}} + (1 - i)x_{1}\bar{x_{2}} + (1 + i)x_{2}\bar{x_{1}} + 2x_{2}\bar{x_{2}}$$