Diagonalization of Matrix

Exercise4-2

1. Determine whether the following matices are diagonalizable. If so find a regular matrix 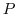$P$ and diagonalize．If not, find an upper triangluar matrix.

(a) $\left(\begin{array}{rr} 1&2\\ 0&-1 \end{array}\right)$ (b) $\left(\begin{array}{rrr} 2&1&1\\ 1&2&1\\ 0&0&1 \end{array}\right)$ (c) $\left(\begin{array}{rrr} 1&1&6\\ -1&3&6\\ 1&-1&-1 \end{array}\right)$

2. Suppose 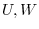$U,W$ are subspaces of the vector space 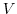$V$. Show that 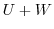$U + W$ is a direct sum if and only if $U \cap W = \{\bf0\}$．

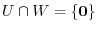3. Let 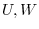$U,W$ be finite dimensional. Then show the following is true.

$$\dim (U \oplus W) = \dim U + \dim W$$

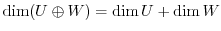
4. For 3 dimensional vector space 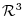${\mathcal R}^{3}$, let

$$U = \{(x_{1},x_{2},x_{3}) : x_{1}+x_{2}+x_{3} = 0\}, W = \{(x_{1},x_{2},x_{3}) : x_{1} = x_{2} = x_{3} \}.$$

Then show that ${\mathcal R}^{3} = U \oplus W$．

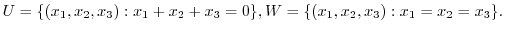
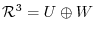5. Show the absolute value of the eigenvalue 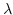$\lambda$ of an orthogonal matrix is $1$．

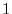6. Suppose that the column vectors of 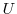$U$ is orthonormal basis. Then show that 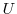$U$ is unitary matrix.