Matrix Transformation

Exercise3-4

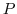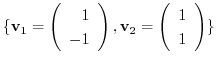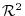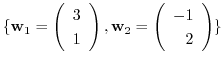1. Find the transposed matrix $P$ which maps the basis $\{{\bf v}_{1} = \left(\begin{array}{r} 1\\ -1 \end{array}\right), {\bf v}_{2} = \left(\begin{array}{r} 1\\ 1 \end{array}\right) \}$ of ${\mathcal R}^{2}$ to the basis $\{{\bf w}_{1} = \left(\begin{array}{r} 3\\ 1 \end{array}\right), {\bf w}_{2} = \left(\begin{array}{r} -1\\ 2 \end{array}\right) \}$ .

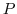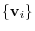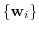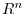2. Show that the transposed matrix $P$ which maps the basis $\{{\bf v}_{i}\}$ to the basis $\{{\bf w}_{i}\}$ of $R^{n}$ is regular .

3. Find all eigenvalues and all eigenvetors of the following matrices．

(a) $\left(\begin{array}{rr} 3&-1\\ 1&1 \end{array}\right)$ (b) $\left(\begin{array}{rrr} 2&1&0\\ 0&1&-1\\ 0&2&4 \end{array}\right)$ (c) $\left(\begin{array}{rrr} 1&4&-4\\ -1&-3&2\\ 0&2&-1 \end{array}\right)$

4. Find the eigenvalue of the square matrix 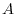$A$ which satisfies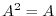 $A^{2} = A$

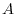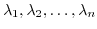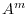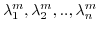5. Let the eigenvalues of $A$ be $\lambda_{1},\lambda_{2},\ldots,\lambda_{n}$ . Then show that the eigenvalues of $A^{m}$ are $\lambda_{1}^{m}, \lambda_{2}^{m}, . . , \lambda_{n}^{m}$ .

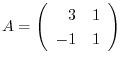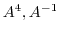6. Given $A = \left(\begin{array}{rr} 3&1\\ -1&1 \end{array}\right)$ . Find $A^{4},A^{-1}$ using Cayley-Hamilton theorem.

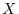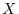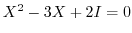7. Suppose $X$ is the matrix of order 2. Find all $X$ satisfying $X^{2} - 3X + 2I = 0$ ．