Linear Mapping

Exercise3-2

1. Determine whether the following mapping is linear mapping.

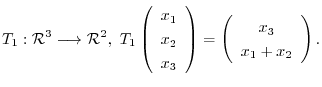
$\displaystyle T_{1} : {\mathcal R}^{3} \longrightarrow {\mathcal R}^{2},\ T_{1}... ...y}\right) = \left(\begin{array}{c} x_{3}\\ x_{1} + x_{2} \end{array}\right) .$

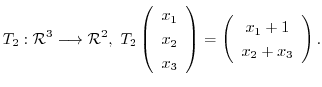
$\displaystyle T_{2} : {\mathcal R}^{3} \longrightarrow {\mathcal R}^{2},\ T_{2}... ...ight) = \left(\begin{array}{c} x_{1} + 1\\ x_{2} + x_{3} \end{array}\right) .$

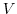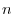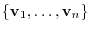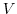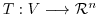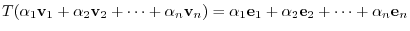2. Let $V$ be the $n$ dimensional vector space. Let $\{{\bf v}_{1},\ldots,{\bf v}_{n}\}$ be the basis of $V$ ．Define $T : V \longrightarrow {\mathcal R}^{n}$ by $T(\alpha_{1}{\bf v}_{1} + \alpha_{2}{\bf v}_{2} + \cdots + \alpha_{n}{\bf v}_{n... ... \alpha_{1}{\bf e}_{1} + \alpha_{2}{\bf e}_{2} + \cdots + \alpha_{n}{\bf e}_{n}$ . Then show that 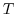$T$ is a linear mapping.

3. Let 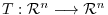$T : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{n}$ be a linear mapping. Then the followings are equivalent.

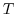(a): is isomorphic．
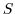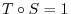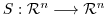(b): There exists such that $T \circ S = 1$ and $S : {\mathcal R}^{n} \longrightarrow {\mathcal R}^{n}$ ．

4. Suppose that 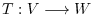$T : V \longrightarrow W$ is a linear mapping. Show that 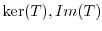$\ker(T),Im(T)$ are the subspace of $V, W$ ．

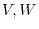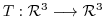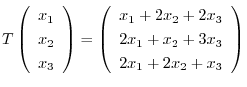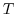5. Let $T : {\mathcal R}^{3} \longrightarrow {\mathcal R}^{3}$ be a linear transformation such that $T\left(\begin{array}{r} x_{1}\\ x_{2}\\ x_{3} \end{array}\right) = \left(\beg... ...x_{3}\\ 2x_{1} + x_{2} + 3x_{3}\\ 2x_{1} + 2x_{2} + x_{3} \end{array}\right)$ . Find the matrix representation $[T]$ of $T$ relative to the usual basis 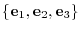$\{{\bf e}_{1},{\bf e}_{2},{\bf e}_{3}\}$ . 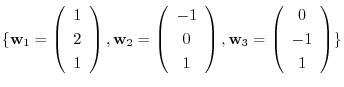Find also $[T]_{\bf w}$ relative to the basis $\{{\bf w}_{1} = \left(\begin{array}{c} 1\\ 2\\ 1 \end{array}\right), {\bf w}_... ...\right), {\bf w}_{3} = \left(\begin{array}{c} 0\\ -1\\ 1 \end{array}\right)\}$ ．