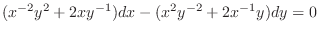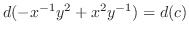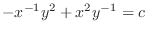Next: Linear Differential Equations Up: 1st order linear differential Previous: Exact Differential Equations 目次 索引
2. Solve the following initial value problem.
Answer
1.
(a) Note that
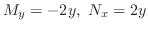 . Then it is not exact differential equation. So, we seek an integrating factor. Since
. Then it is not exact differential equation. So, we seek an integrating factor. Since
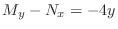 , calculate
, calculate
![$(1/N)[M_{y} - N_{x}]$](img311.png) . Then
. Then
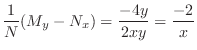
 only. Thus, the integrating factor is given by
only. Thus, the integrating factor is given by
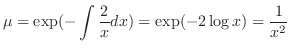
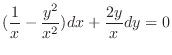
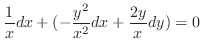
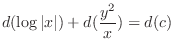
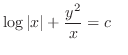
(b) Note that
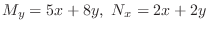 . Thus it is not exact. So, we seek an integrating factor. Since
. Thus it is not exact. So, we seek an integrating factor. Since
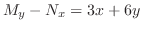 , calculate
, calculate
![$(1/N)[M_{y} - N_{x}]$](img311.png) . Then we have
. Then we have
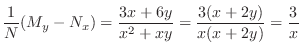
 only. So, the integrating factor is given by
only. So, the integrating factor is given by
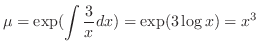
 to the original euqation, w have
to the original euqation, w have
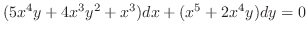
![$\displaystyle x^3 dx + [(5x^4 y + 4x^3 y^2) dx + (x^5 + 2x^4 y ) dy] = 0 $](img324.png)
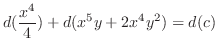
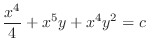
(c) Note that
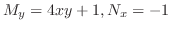 . Then it is not exact. So, we look for an integrating factor. Since
. Then it is not exact. So, we look for an integrating factor. Since
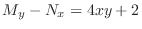 , we calculate
, we calculate
![$(1/M)[M_{y} - N_{x}]$](img329.png) . Then
. Then
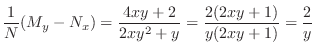
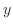 only. Thus the integrating factor is given by
only. Thus the integrating factor is given by
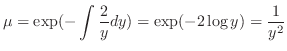
 to the original equation.
to the original equation.
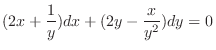
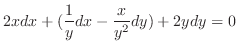
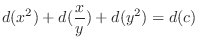
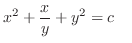
(d) Note that
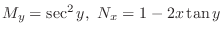 . Then it is not exact. So, we look for an integrating factor.
. Then it is not exact. So, we look for an integrating factor.
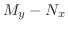 |
 |
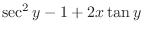 |
|
 |
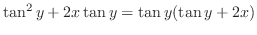 |
![$(1/M)[M_{y} - N_{x}]$](img329.png) , we have
, we have
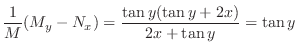
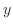 only. Thus the integrating factor is given by
only. Thus the integrating factor is given by
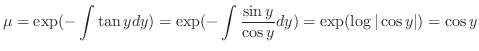
 to the original equation.
to the original equation.
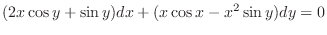
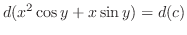
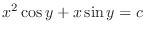
2.
(a) Note that
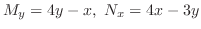 . Then this is not exact. So, we look for an integrating factor.
. Then this is not exact. So, we look for an integrating factor.
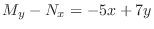
![$(1/N)[M_{y} - N_{x}], (1/M)[M_{y} - N_{x}]$](img347.png) are not function of
are not function of  only. So, we let the integrating factor
only. So, we let the integrating factor
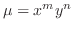 . Then we find
. Then we find 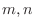 .
.
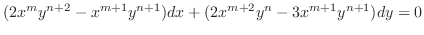
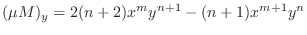
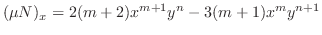
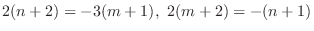
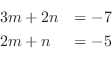
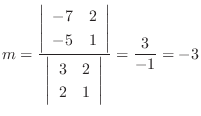
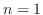 . Thus,
. Thus,
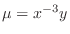 . Now multiply
. Now multiply  to the original equation, we have
to the original equation, we have
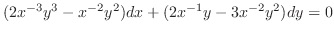
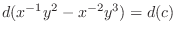
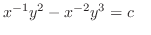
(b) Note that
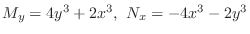 . Thus it is not exact. So, we look for an integrating factor. By the form of
. Thus it is not exact. So, we look for an integrating factor. By the form of
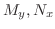 , we assume that
, we assume that
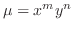 . Then we find
. Then we find 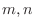 .
.
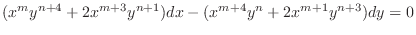
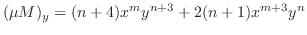
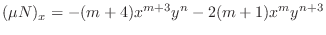
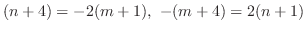
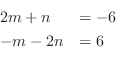
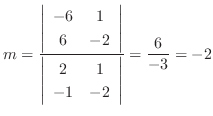
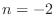 . Thus,
. Thus,
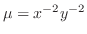 . Multiply
. Multiply  to the original equation. Then we have
to the original equation. Then we have