Next: Integrating Factor Up: 1st order linear differential Previous: Homogeneous Differential Equations 目次 索引
2. Solve the following initial value problems.
(a)
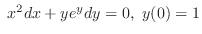
(b)
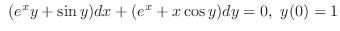
(c)
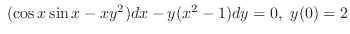
Answer
1.
(a) Since
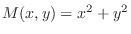 ,
,
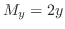 . Also since
. Also since
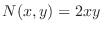 ,
,
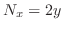 . Then
. Then
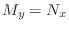 and exact. Now using grouping method, we have
and exact. Now using grouping method, we have
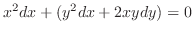
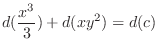
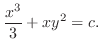
(b) Since
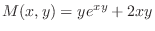 ,
,
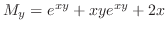 . Also since
. Also since
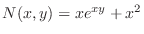 ,
,
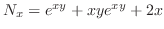 . Thus,
. Thus,
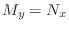 and exact. Now using the initial condition
and exact. Now using the initial condition
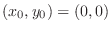 , we have
, we have
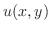 |
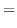 |
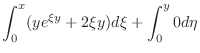 |
|
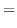 |
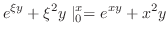 |
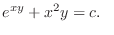
(c) Since
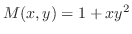 ,
,
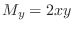 . Also since
. Also since
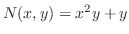 ,
,
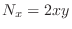 . Thus,
. Thus,
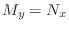 and exact. Now using grouping method, we have
and exact. Now using grouping method, we have
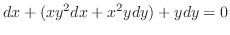
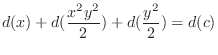
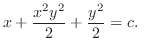
(d) Since
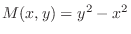 ,
,
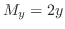 . Also since
. Also since
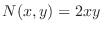 ,
,
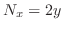 . Thus,
. Thus,
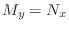 and exact. Now using the grouping method, we have
and exact. Now using the grouping method, we have
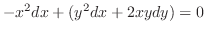
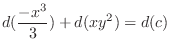
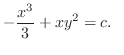
2.
(a) Since
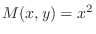 ,
,  . Also since
. Also since
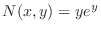 ,
, 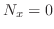 . Thus,
. Thus,
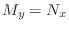 and exact. Here using the grouping method, we have
and exact. Here using the grouping method, we have
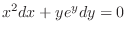
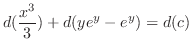
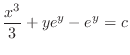
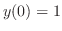 , we have
, we have
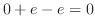 and
and
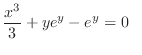
Alternate Solution
Since
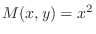 ,
,  . Also since
. Also since
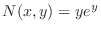 ,
, 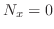 . Thus,
. Thus,
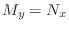 and exact. Now set
and exact. Now set
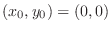 . Then we have
. Then we have
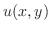 |
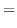 |
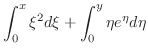 |
|
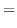 |
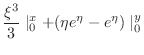 |
||
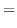 |
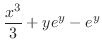 |
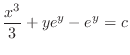
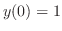 , we have
, we have
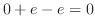 and
and
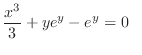
(b) Since
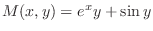 ,
,
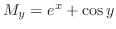 . Also since
. Also since
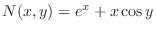 ,
,
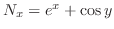 . Thus,
. Thus,
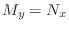 and exact. Set
and exact. Set
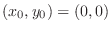 . Then we have
. Then we have
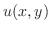 |
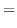 |
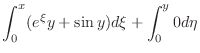 |
|
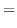 |
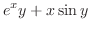 |
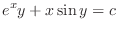
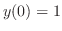 , we have
, we have 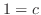 and
and
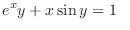
(c) Since
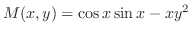 ,
,
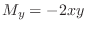 . Also since
. Also since
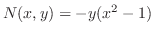 ,
,
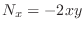 . Thus,
. Thus,
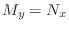 and exact. Using the grouping method, we have
and exact. Using the grouping method, we have
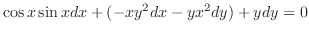
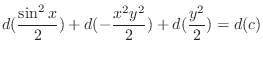
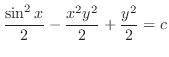
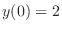 , we have
, we have
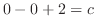 and
and