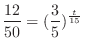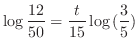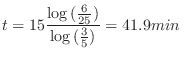Next: Homogeneous Differential Equations Up: 1st order linear differential Previous: Differential equations 目次 索引
(a)
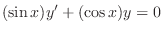
(b)
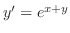
(c)
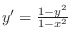
(d)
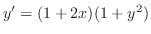
2. Solve the following initial problem.
(a)
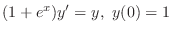
(b)
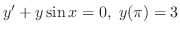
(c)
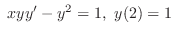
(d)
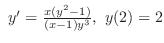 3.
3.
We took out the object which is
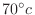 to the outside whose temperature is
to the outside whose temperature is
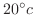 . After 15 minutes, the object temperature was
. After 15 minutes, the object temperature was
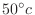 . Answer the following questions
. Answer the following questions
(a) Find the object's temperature after 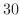 minutes.
minutes.
(b) Find the time it takes for the temperature of object to reach
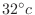 .
.
Answer
1.
(a) Separate the variables.
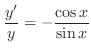
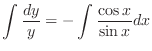
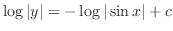
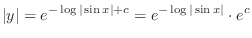
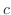 is an arbitrary constant. So, we write
is an arbitrary constant. So, we write 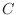 for
for 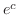 .
Therefore,
.
Therefore,
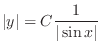
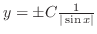 . But
. But 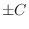 is again a constant. So, we use
is again a constant. So, we use 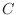 .
.
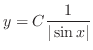
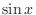 , then we have
, then we have
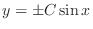 . But
. But 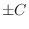 is again a constant. So, we use
is again a constant. So, we use 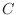 . Then
. Then
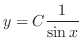
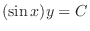
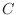 in this way is called abuse of
in this way is called abuse of 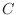 . From now on we do use the abuse of
. From now on we do use the abuse of 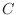 without telling you.
without telling you.
(b) Separating the variables, we have
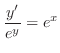
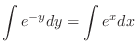
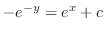
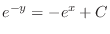
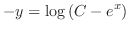
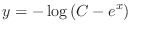
(c) Separate the variables and integrate both sides, we have
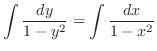
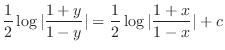
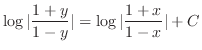
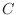 , we have
, we have
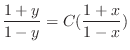
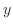 ,
,
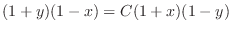
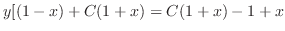
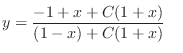
(d) Separate the variables and integrate both sides,
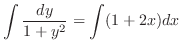
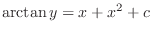
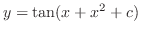
2. (a) Separate the variables and integrate both sides,
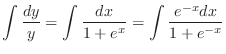
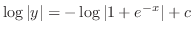
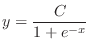
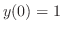 . Then
. Then
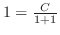 and
and
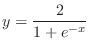
(b) Separate the variables and integrate both sides,
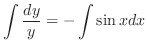
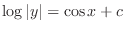
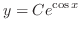
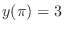 , we have
, we have
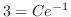 and
and
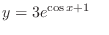
(c) Separate the variables and integrate both sides,
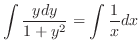
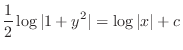
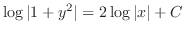
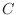 , we have
, we have
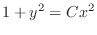
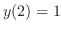 , we have
, we have
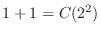 and
and
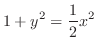
(d) Separating the variables, we have
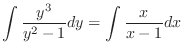
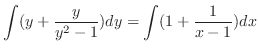
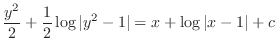
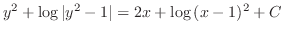
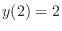 . Then
. Then
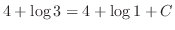 implies that
implies that
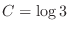 .
Therefore,
.
Therefore,
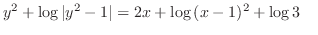
3. (a) Using the Newton's cooling law, we have

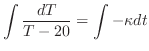
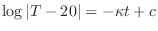
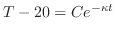
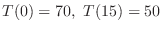 . Then
. Then
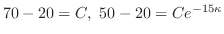 より
より
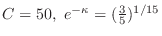 . Thus,
. Thus,
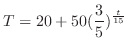
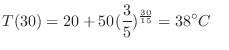
(b) Since the object's temperature is
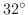 ,
,
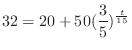
 . Then
. Then