Next: 索引 Up: Solution by Series Previous: Anslytic Functions 目次 索引
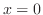 .
.
(a)
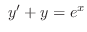
(b)
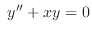
(c)
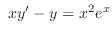
(d)
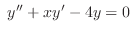
2. Find the series solution of the following differential equations about the indicated point.
4.2
1.
(a) Since
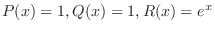 ,
,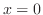 is an ordinary point. Thus, we set the solution
is an ordinary point. Thus, we set the solution
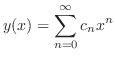
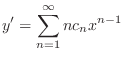
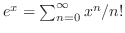 , we substitute this into the given equation. Then
, we substitute this into the given equation. Then
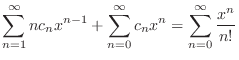
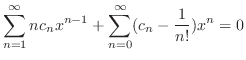
 to be the least power
to be the least power 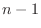 .
.
![$\displaystyle \sum_{n=1}^{\infty}[nc_{n} + c_{n-1} - \frac{1}{(n-1)!}]x^{n-1} = 0 . $](img1608.png)
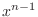 are all 0. Thus, we have
are all 0. Thus, we have
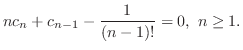
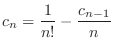
Now that the value of 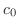 is determined by
is determined by 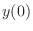 . In this case,
. In this case, 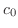 is treated as constant. Thus, we find
is treated as constant. Thus, we find
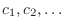 . Then
. Then
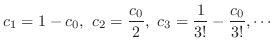
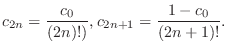
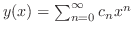 . Then
. Then
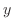 |
 |
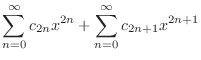 |
|
 |
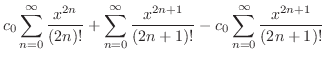 |
||
 |
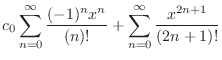 |
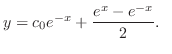
(b) Since
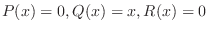 ,
,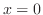 is an ordinary point. Then we set our solution as
is an ordinary point. Then we set our solution as
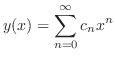
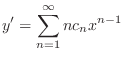
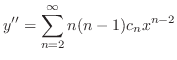
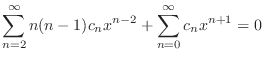
 to be the smallest
to be the smallest 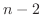 . Then
. Then
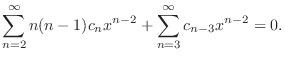
![$\displaystyle 2c_{2} + \sum_{n=3}^{\infty}[n(n-1)c_{n} + c_{n-3}]x^{n-2} = 0 $](img1628.png)
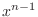 are all 0. Then we have the following recurrence relation.
are all 0. Then we have the following recurrence relation.
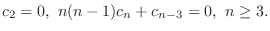
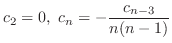
Note that the value of
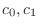 are determined by
are determined by
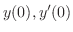 . So, we can think of them as constants. Thus, we find
. So, we can think of them as constants. Thus, we find
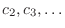 interms of
interms of 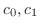 .
.
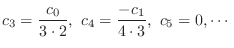
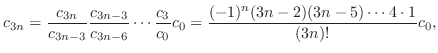
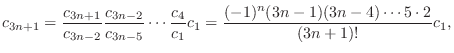
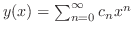 . Then
. Then
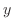 |
 |
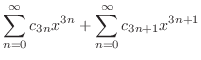 |
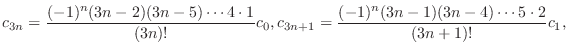
(c) Since
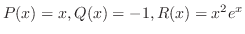 ,
,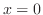 is an ordinary point. Then we set
is an ordinary point. Then we set
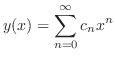
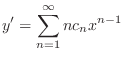
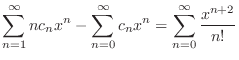
 to be the least
to be the least 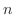 . Then
. Then
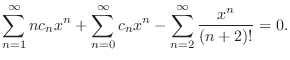
![$\displaystyle c_{1}x - c_{0} - c_{1}x + \sum_{n=2}^{\infty}[nc_{n} - c_{n} - \frac{1}{(n-2)!}]x^{n} = 0. $](img1644.png)
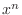 are all 0. Thus, we have the recurrence relation.
are all 0. Thus, we have the recurrence relation.
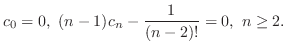
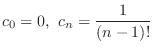
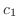 is determined by the initial condition
is determined by the initial condition
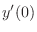 . Thus, we can think of
. Thus, we can think of 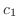 as a constant.
as a constant.
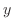 |
 |
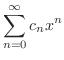 |
|
 |
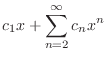 |
||
 |
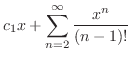 |
||
 |
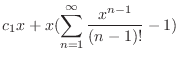 |
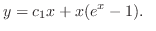
(d) Since
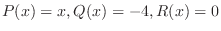 ,
,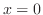 is an ordinary point. Thus we set
is an ordinary point. Thus we set
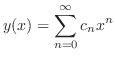
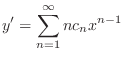
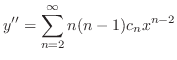
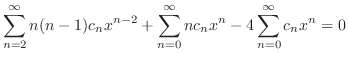
 to the least
to the least 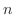 .
.
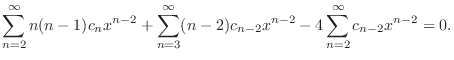
![$\displaystyle 2c_{2} - 4c_{0} + \sum_{n=3}^{\infty}[n(n-1)c_{n} + (n-6)c_{n-2}]x^{n-2} = 0. $](img1658.png)
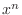 are all 0. So, we have the recurrent equation.
are all 0. So, we have the recurrent equation.
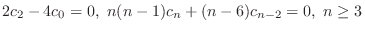
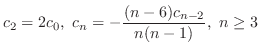
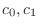 are determined by
are determined by
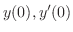 . Then we can think of these as arbitrary constants. Thus, we find
. Then we can think of these as arbitrary constants. Thus, we find
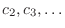 interms of
interms of 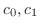 . Now
. Now
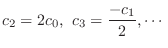
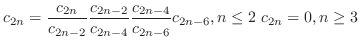
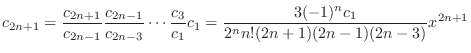
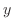 |
 |
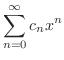 |
|
 |
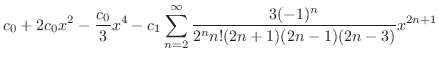 |
2.
(a) Since
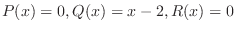 ,
,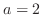 is an ordinary point. Then we let the solution
is an ordinary point. Then we let the solution
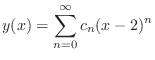
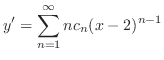
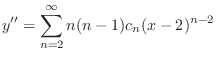
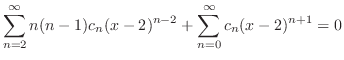
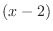 to the least
to the least 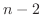 . Then
. Then
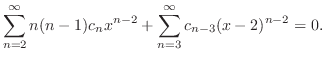
^{n-2} = 0. $](img1673.png)
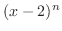 are all 0. Thus, we have the recurrence relation.
are all 0. Thus, we have the recurrence relation.
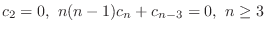
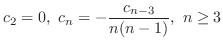
Note that
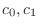 are determined by
are determined by
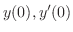 . Then we can think of these as arbitrary constants. Thus, we find
. Then we can think of these as arbitrary constants. Thus, we find
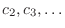 interms of
interms of 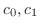 . Now
. Now
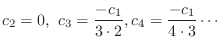
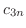 |
 |
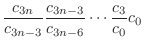 |
|
 |
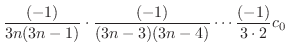 |
||
 |
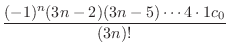 |
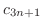 |
 |
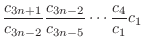 |
|
 |
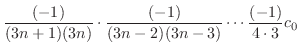 |
||
 |
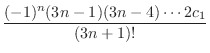 |
||
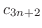 |
 |
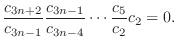 |
 |
 |
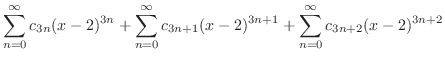 |
|
 |
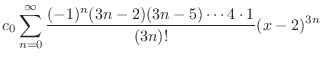 |
||
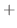 |
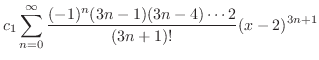 |
(b) Since
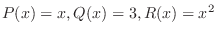 ,
,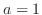 is an ordinary point. Then let
is an ordinary point. Then let
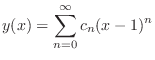
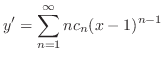
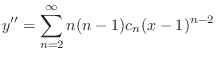
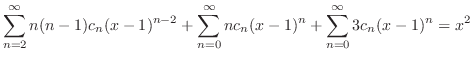
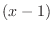 to the least
to the least 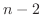 . ,
. ,
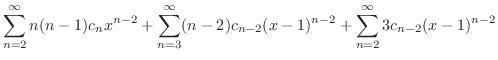 |
|||
 |
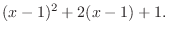 |
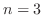 . Then
. Then
^{n-2} = (x-1)^2 + 2(x-1) + 1. $](img1701.png)
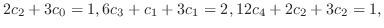
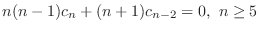
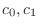 are determined by
are determined by
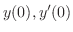 . Then we can think of these as arbitray constants. Thus, we find
. Then we can think of these as arbitray constants. Thus, we find
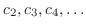 interms of
interms of 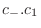 . Then we have
. Then we have
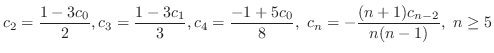
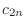 |
 |
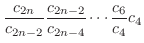 |
|
 |
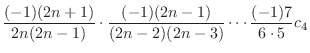 |
||
 |
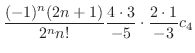 |
||
 |
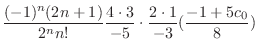 |
||
 |
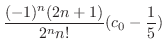 |
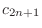 |
 |
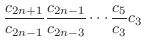 |
|
 |
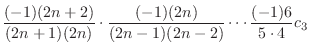 |
||
 |
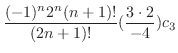 |
||
 |
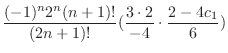 |
||
 |
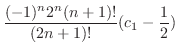 |
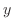 |
 |
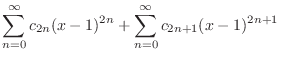 |
|
 |
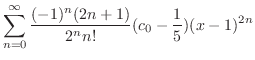 |
||
 |
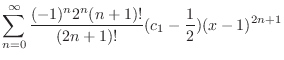 |