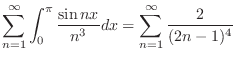Next: Series Solution(case of ordinary Up: Solution by Series Previous: Solution by Series 目次 索引
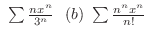
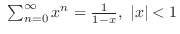
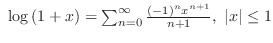
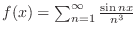 ,Show the followings.
,Show the followings.
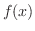 is uniformly convergent on
is uniformly convergent on
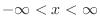 .
.
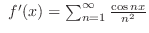
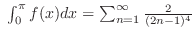
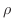 |
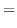 |
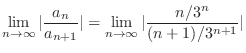 |
|
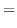 |
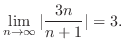 |
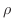 |
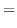 |
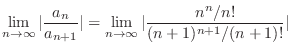 |
|
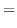 |
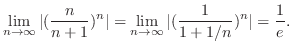 |
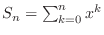 . Then
. Then
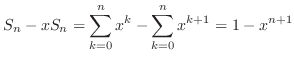
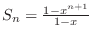 . Note that
. Note that
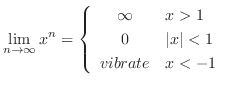
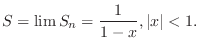
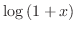 |
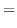 |
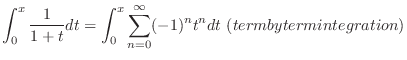 |
|
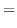 |
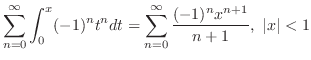 |
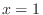 ,
,
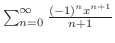 converges.
converges.
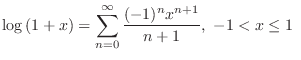
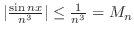 .
.
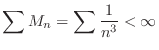
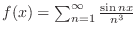 . Then
. Then
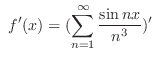
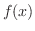 is uniformly convergent. Thus term by term differentiation is possible. Thus,
is uniformly convergent. Thus term by term differentiation is possible. Thus,
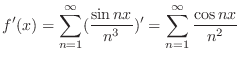
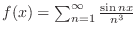 . Then
. Then
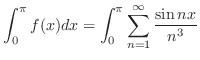
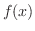 is uniformly convergent. Thus, term by term integration is possible. Therefore,
is uniformly convergent. Thus, term by term integration is possible. Therefore,