Next: Exercise Up: Power series solution of Previous: Exercise Contents Index
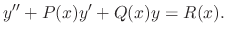
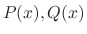 , and
, and 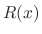 area analytic at
area analytic at 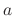 , then we call
, then we call 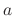 ordinary point.
ordinary point.
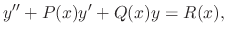
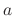 is an ordinary point, then for any
is an ordinary point, then for any
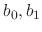 , the initial value problem
, the initial value problem
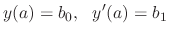
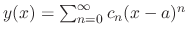 .
.
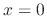
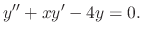
SOLUTION
Since
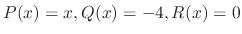 ,
, 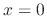 is an ordinary point.
Now let
is an ordinary point.
Now let
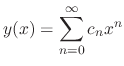
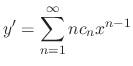
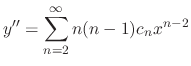
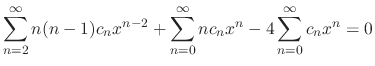
 be the least number
be the least number 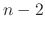 .C
.C
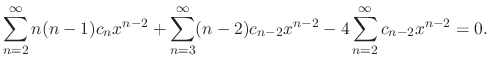
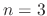 . Then
. Then
![$\displaystyle 2c_{2} - 4c_{0} + \sum_{n=3}^{\infty}[n(n-1)c_{n} + (n-6)c_{n-2}]x^{n-2} = 0. $](img1256.png)
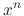 are all 0. Thus
are all 0. Thus
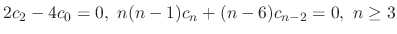
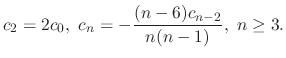
Here,
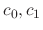 can be decided by the initial conditions
can be decided by the initial conditions
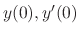 . Thus, we can think of these as constants. Now we find
. Thus, we can think of these as constants. Now we find
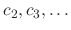 . Then
. Then
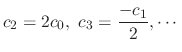
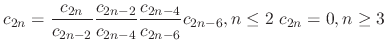
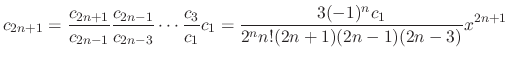
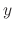 |
 |
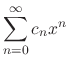 |
|
 |
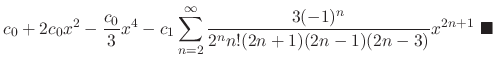 |