Next: Power series solution (Ordinary Up: Analytic functions Previous: Analytic functions Contents Index
1. Find the radius of convergence of the following power series.
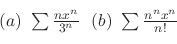
2. Show the following.
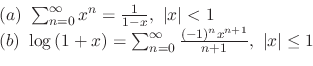
3. Suppose that
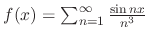 . Then show the following.
. Then show the following.
(a) 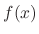 is uniformly convergent on is uniformly convergent on
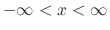 . . |
(b)
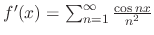 |
(c)
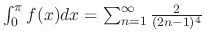 |