Next: Separation of variables Up: Differential Equations Previous: Differential Equations Contents Index
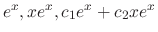 are solutions of the differential equation
are solutions of the differential equation
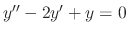 . For
. For
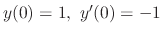 , find
, find
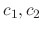 .
.
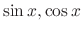 and their linear combinations are solutions to the differential equation
and their linear combinations are solutions to the differential equation
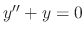 .
What can you say about the vector space spanned by
.
What can you say about the vector space spanned by
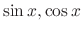 .
.