Next: Exercise Up: 1st Order Differential Equation Previous: 1st Order Differential Equation Contents Index
Many natural laws in Physics, Chemistry, and Engineering are expressed by means of differential equations. Among many natural laws, we treat Newton's 2nd law, Newton's cooling law, Kirchhoff's 2nd law, Fourier's law of heat transfer, wave equation, chemical equation.
A differential equation is a relation between an unknown function and derivatives of the unknown function. Differential equations we treat are the ones that can be solved by quadrature.
A relation among an independent variable  , and a function
, and a function 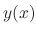 ,
,
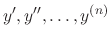 expressed in
expressed in
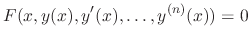
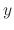 .
.
We give some examples of differential equations.
Note that
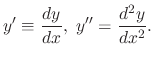
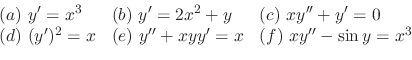
The order of the differential equation is the highest order derivative present in the differential equation.
Differential equations
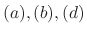 are the 1st order and the rest is 2nd order.
The natural laws we mentioned above are formulated as the 1st order or the 2nd order differential equation. In this book, we deal mainly with the 1st and the 2nd order differential equations.
are the 1st order and the rest is 2nd order.
The natural laws we mentioned above are formulated as the 1st order or the 2nd order differential equation. In this book, we deal mainly with the 1st and the 2nd order differential equations.
A differential equation is called linear if the equation is expressed as an unknown function and it's derivatives. Otherwise it is called non linear. Thus, 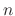 th order linear differential equation is expressed in the following form.
th order linear differential equation is expressed in the following form.
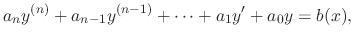
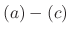 are linear,
are linear, 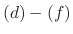 are non linear.
are non linear.
If a function saitisfies the given differential equation on some interval, then the function is called the solution of the differential equation. To find a solution of the given differential equation, we say solve the differential equation. A solution may not be in the form of 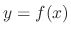 . It sometimes given by implicit function such as
. It sometimes given by implicit function such as
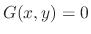 .
.
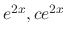 are solutions of
are solutions of
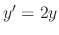 . Show the functions
. Show the functions
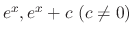 are not solution of
are not solution of
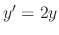 .
.
SOLUTION
The derivatives of 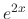 and
and 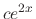 are
are 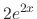 and
and 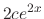 respectively. Thus these satisfy
respectively. Thus these satisfy
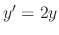 .
Since
.
Since
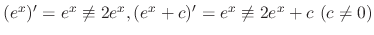 . Thus they are not the solutions of
. Thus they are not the solutions of
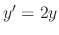

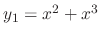 and
and
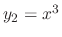 are solutions of
are solutions of
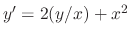 .
.
SOLUTION
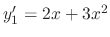 and
and
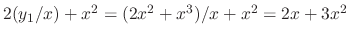 . Thus,
. Thus, 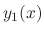 is a solution. Similarly,
is a solution. Similarly,
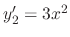 and
and
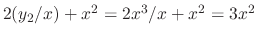 . Thus,
. Thus, 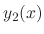 is a solution
is a solution

As you can see from this example, solutions of a differential equation may not be unique. In general, any 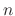 th order differential equation has
th order differential equation has 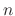 different solutions.
different solutions.
We say a linear combination of 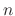 independent solutions of
independent solutions of 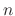 constants the general solution.
constants the general solution.
Any solution derived from substituting a particular value into the general solution is called the particular solution.
For example,
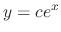 is the general solution of
is the general solution of
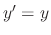 and
and 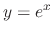 is the particular solution.
is the particular solution.
A singular solution is a solution which can not be derived from substituting a value into the general solution.
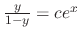 is the general solution of
is the general solution of
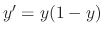 . Then show no matter what value you choose for
. Then show no matter what value you choose for 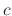 ,
, 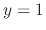 can not be obtained. Show
can not be obtained. Show 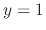 is the singular solution.
is the singular solution.
SOLUTION
Differentiate
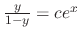 with respect to
with respect to  . Then
. Then
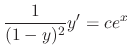
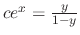 , we have
, we have
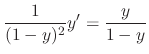
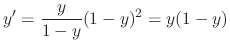
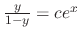 is the general solution.
Now
is the general solution.
Now 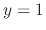 can not be derived from the general solution. Thus
can not be derived from the general solution. Thus 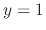 is the singular solution.
is the singular solution.
Note that the general solution of a differential equation forms curves. A each curve is called the solution curve or the integral curve.
In a differential equation
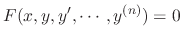 , initial conditions are values of the solution and its derivatives at specific points such as
, initial conditions are values of the solution and its derivatives at specific points such as
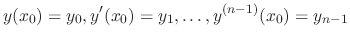
In a differential equation
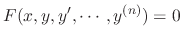 on
on ![$[a,b]$](img46.png) , the condition must be satisfied by the solution or the derivatives of the solution is called the boundary conditions.
The problem of finding a solution to the differential equation with the boundary conditions is called the boundary value problem
, the condition must be satisfied by the solution or the derivatives of the solution is called the boundary conditions.
The problem of finding a solution to the differential equation with the boundary conditions is called the boundary value problem