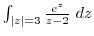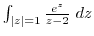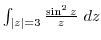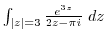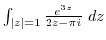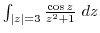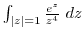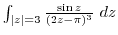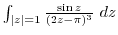Cauchy's integral formula

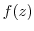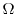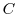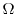Theorem 4..3 (Integral formula of holomorphic function)   Suppose the function $f(z)$ is regular in the region $\Omega$. When there is a single closed curve $C$ in $\Omega$ and the inside of 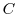$C$ is also contained in 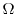$\Omega$, the following formula for any point 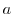$a$ inside 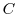$C$ Holds.

$$f(a) = \frac{1}{2\pi i}\int_{C}\frac{f(z)}{z-a};dz$$

$$f^{(n)}(a) = \frac{n!}{2\pi i}\int_{C}\frac{f(z)}{(z-a)^{n+1}}\;dz$$

Exercise4.4

1. Prove the following formula.

$$f^{(n)}(a) = \frac{n!}{2\pi i}\int_{C}\frac{f(z)}{(z-a)^{n+1}} dx (n = 1,2,3,\ldots)$$

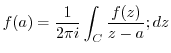
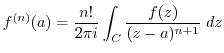
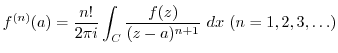
2. Evaluate the following integrals.

(a)

$\int_{\vert z\vert=3}\frac{e^{z}}{z - 2} dz$

(b)

$\int_{\vert z\vert=1}\frac{e^{z}}{z - 2} dz$

(c)

$\int_{\vert z\vert=3}\frac{\sin^{2}{z}}{z} dz$

(d)

$\int_{\vert z\vert=3}\frac{e^{3z}}{2z - \pi i} dz$

(e)

$\int_{\vert z\vert=1}\frac{e^{3z}}{2z - \pi i} dz$

(f)

$\int_{\vert z\vert=3}\frac{\cos{z}}{z^2 + 1} dz$

(g)

$\int_{\vert z\vert=1}\frac{e^{z}}{z^{4}} dz$

(h)

$\int_{\vert z\vert=3}\frac{\sin{z}}{(2z - \pi)^{3}} dz$

(i)

$\int_{\vert z\vert=1}\frac{\sin{z}}{(2z - \pi)^{3}} dz$