Next: 5.1 Laurent expansion Up: Solution Previous: 4.3 Cauchy's integral theorem Index
2. Cauchy's integral formula
If 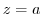 is inside of the curve
is inside of the curve  and
and  is analytic inside of the region containing curve
is analytic inside of the region containing curve  , then
, then
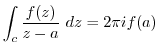
Cauchy's integral theorem
If
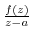 is analytic inside of curve
is analytic inside of curve  , then
, then
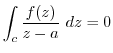
(a)
Since 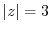 ,
, 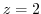 is inside of this curve. Then by Cauchy's integral formula, we have
is inside of this curve. Then by Cauchy's integral formula, we have
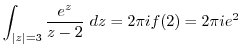
(b) Since 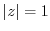 ,
, 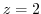 is not inside of this circle. Then the integrand is analytic. Thus by Cauchy's integral theorem,
is not inside of this circle. Then the integrand is analytic. Thus by Cauchy's integral theorem,
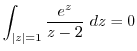
(c) Since 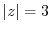 ,
, 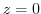 is inside of this circle. Then by Cauchy's integral formula,
is inside of this circle. Then by Cauchy's integral formula,
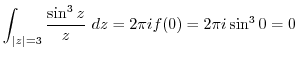
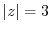 ,
,
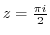 is inside of this circle. Then by Cauchy's integral formula,
is inside of this circle. Then by Cauchy's integral formula,
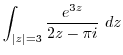 |
 |
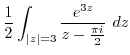 |
|
 |
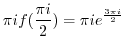 |
||
 |
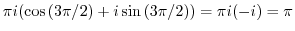 |
(e) Since 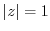 ,
,
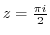 is not inside of this circle. Then the integrand is analytic. Thus by Cauchy's integral theorem,
is not inside of this circle. Then the integrand is analytic. Thus by Cauchy's integral theorem,
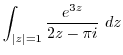 |
 |
0 |
(f) Since 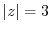 ,
, 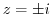 is inside of this circle. Then by Cauchy's integral formula,
is inside of this circle. Then by Cauchy's integral formula,
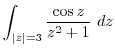 |
 |
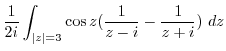 |
|
 |
![$\displaystyle \frac{1}{2i}[2\pi i (f(i) - f(-i))] = \pi[\cos{(i)} - \cos{(-i)}]$](img961.png) |
||
 |
![$\displaystyle \pi[\frac{e^{i^2} + e^{-i^2}}{2} - (\frac{e^{-i^2} + e^{i^2}}{2})] = 0$](img962.png) |
(g) Since 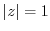 ,
, 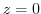 is inside of this circle. Then by Cauchy's integral formula,
is inside of this circle. Then by Cauchy's integral formula,
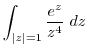 |
 |
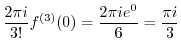 |
(h) Since 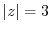 ,
,
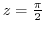 is inside of thie circle. Then by Cauchy's integral formula,
is inside of thie circle. Then by Cauchy's integral formula,
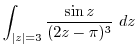 |
 |
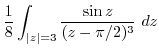 |
|
 |
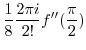 |
Note that
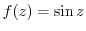 ,
,
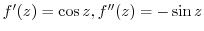 . Then
. Then
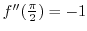 . Thus
. Thus
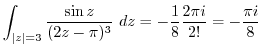
(i) Since 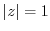 ,
,
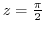 is not inside of thie circle. Then the integrand is analytic. Thus by Cauchy's integral theorem,
is not inside of thie circle. Then the integrand is analytic. Thus by Cauchy's integral theorem,
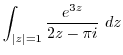 |
 |
0 |