2.3 Higher order derivatives

=2.6zw =1(a) Use mathematical induction．For 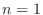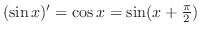$n = 1$ ， $(\sin{x})^{\prime} = \cos{x} = \sin(x + \frac{\pi}{2})$ . Now assume the claim is true for 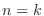$n = k$ and show that the claim is true for $n = k+1$ ．
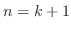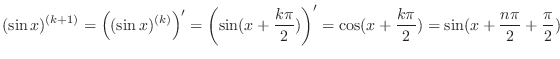
$\displaystyle{(\sin{x})^{(k+1)} = \left((\sin{x})^{(k)}\right)^{\prime} = \left... ...{\prime} = \cos(x + \frac{k\pi}{2}) = \sin(x + \frac{n\pi}{2} + \frac{\pi}{2})}$

=2.6zw =1(b) For 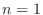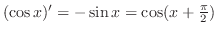$n = 1$ ， $(\cos{x})^{\prime} = -\sin{x} = \cos(x + \frac{\pi}{2})$ . Assume that it is true for 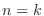$n = k$ and show that true for $n = k+1$ ．
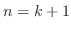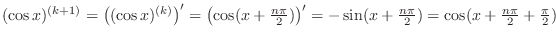
$(\cos{x})^{(k+1)} = \left((\cos{x})^{(k)}\right)^{\prime} = \left(\cos(x + \fra... ...{\prime} = -\sin(x + \frac{n\pi}{2}) = \cos(x + \frac{n\pi}{2} + \frac{\pi}{2})$

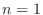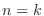=2.6zw =1(c) For $n = 1$ ， $[(1+x)^{\alpha}]^{\prime} = \alpha(1+x)^{\alpha-1}$ . Next assume that claim is true for $n = k$ . Then show it is true for $n = k+1$ ．

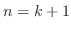$\displaystyle [(1+x)^{\alpha}]^{(k+1)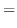}$	$\displaystyle =$	$\displaystyle \left([(1+x)^{\alpha}]^{(k)}\right)^{\prime} = \left(\alpha(\alpha-1)\cdots (\alpha - k +1)(1+x)^{\alpha -k}\right)^{\prime}$
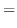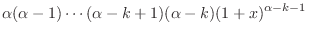	$\displaystyle =$	$\displaystyle \alpha(\alpha-1)\cdots (\alpha - k +1)(\alpha -k)(1+x)^{\alpha - k-1}$

(a) $\displaystyle{f^{(n)}(x) = \left\{\begin{array}{ll} -2x - 1 + (1-x)^{-2}, & n ... ... -2 + 2(1-x)^{-3}, & n = 2\\ n!(1-x)^{-n-1}, & n \geq 3 \end{array}\right.}$

(b) $\displaystyle{x^2 \sin{\left(x + \frac{n\pi}{2}\right)} + 2xn\sin{\left(x + \frac{(n-1)\pi}{2}\right)} + n(n-1)\sin{\left(x + \frac{(n-2)\pi}{2}\right)}}$