Next: 1.5 Sequences Up: ANSWERS B Previous: 1.3 Limits Contents Index
1.
(a) does not exist (b) 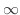 (c)
(c) 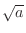 (d)
(d) 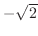 (e)
(e) 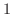 (f) 0(g) does not exist
(f) 0(g) does not exist
2.
3.
For
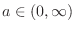 , show
, show
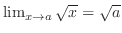 .For all positive number
.For all positive number
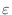 ,let
,let
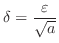 ,then
,then
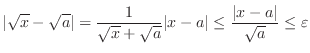
4.
5.
Put
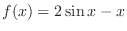 . Then
. Then 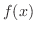 is continous at
is continous at
![$\displaystyle{[\frac{\pi}{2},\pi]}$](img2050.png) and
and
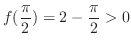 . Since
. Since
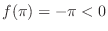 , by the intermediate value theorem,
there exists
, by the intermediate value theorem,
there exists 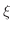 in
in
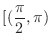 satisfying
satisfying
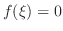 .
.