Next: Conditional Extrema Up: Extreme Values of Function Previous: Extreme Values of Function Contents Index
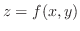 by a quadratic polynomial of
by a quadratic polynomial of  and
and  .
.
| Aroximation |
|---|
Note that the total differential is an approximation of the surface
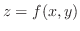 at at 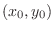 by the tangent plane. If we approximate the surface by the quadratic polynomial, we expect better approximation. by the tangent plane. If we approximate the surface by the quadratic polynomial, we expect better approximation.
|
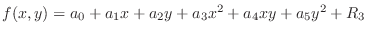 , where
, where 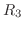 is an error term. Then find all 2nd order partial derivatives of
is an error term. Then find all 2nd order partial derivatives of
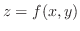 . If
. If 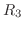 is so small that we can neglect, then
is so small that we can neglect, then
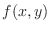 |
 |
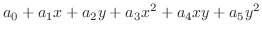 |
|
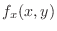 |
 |
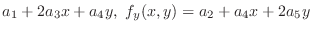 |
|
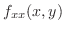 |
 |
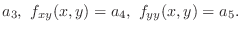 |
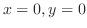 . Then
. Then
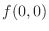 |
 |
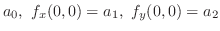 |
|
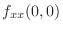 |
 |
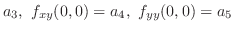 |
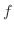 by the 2nd order partial derivatives. Therefore,
by the 2nd order partial derivatives. Therefore,
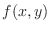 |
 |
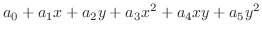 |
|
 |
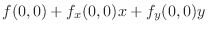 |
||
 |
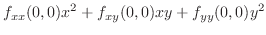 |
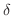 neighborhood neighborhood |
|---|
A 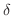 neighborhood of neighborhood of 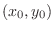 is a set of is a set of 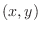 such that such that
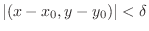 . .
|
| Partial Differential Operator |
|---|
Let 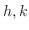 be constants, We define be constants, We define
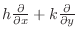 by by
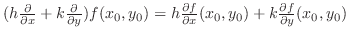 . .
|
NOTE Let
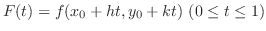 . Then
. Then 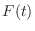 is the class
is the class 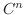 in
in 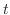 . Thus by Maclausin theorem,
. Thus by Maclausin theorem,
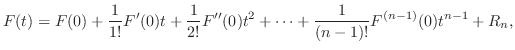
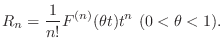
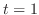 ,
,
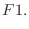 |
 |
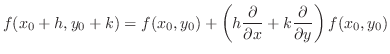 |
|
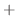 |
 |
||
 |
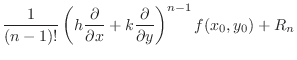 |
| Maclaurin Theorem |
|---|
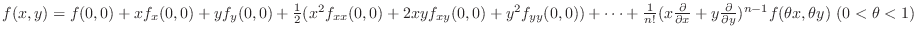
|
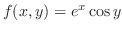 . Find the Taylor polynomial of 2nd degree at
. Find the Taylor polynomial of 2nd degree at 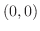 .
.
By Maclaurin theorem,
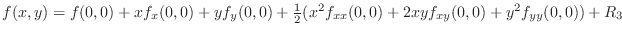 s.
s.
SOLUTION We first find all 2nd partial derivatives of
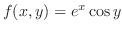 .
.
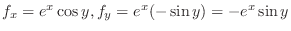 ,
,
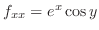 ,
,
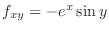 ,
,
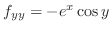 . Theorem4.7, let
. Theorem4.7, let
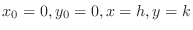 . Then
. Then
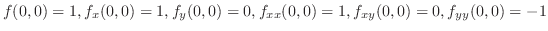 . Thus
. Thus
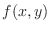 |
 |
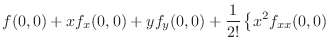 |
|
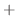 |
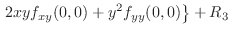 |
||
 |
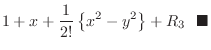 |
| Exercise4-16 |
|---|
Note that Taylor polynomial of 2nd degree of a function at
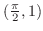 means expressing the function using means expressing the function using
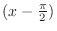 and and 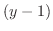 . .
|
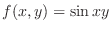 at
at
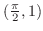 .
.
SOLUTION
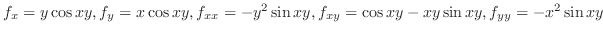 . Thus in Theorem4.7, let
. Thus in Theorem4.7, let
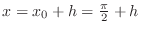 ,
,
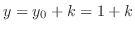 . Then
. Then
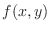 |
 |
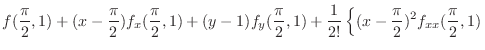 |
|
 |
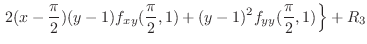 |
||
 |
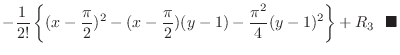 |
Proof
By Taylor theorem, for
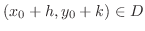 ,
we have
,
we have
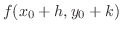 |
 |
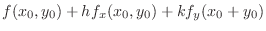 |
|
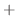 |
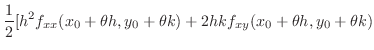 |
||
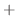 |
![$\displaystyle k^2 f_{yy} (x_{0}+\theta h,y_{0}+\theta k)], (0 < \theta < 1)$](img702.png) |
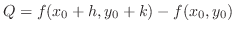 . Then
. Then
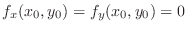 and
and
![$\displaystyle Q = \frac{1}{2}[h^2 f_{xx}(x_{0}+\theta h,y_{0}+\theta k) + 2hkf_...
...x_{0}+\theta h,y_{0}+\theta k) + k^2 f_{yy} (x_{0}+\theta h,y_{0}+\theta k) ]. $](img705.png)
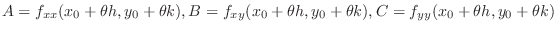 . Then
. Then
![$\displaystyle Q = \frac{1}{2}\left(Ah^2 + 2Bhk + Ck^2\right) = \frac{A}{2}\left[(h + \frac{Bk}{A})^2 + \frac{(AC - B^2)k^2}{A^2}\right]. $](img707.png)
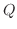 is determinde by the sign of
is determinde by the sign of 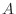 and the sign of
and the sign of 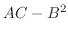 .
.
1. If
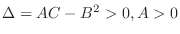 , then since
, then since  is the class
is the class 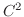 function, for any
function, for any 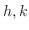 such that
such that 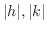 is sufficiently small and never 0 simulteneously, we have
is sufficiently small and never 0 simulteneously, we have 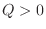 . Thus,
. Thus,
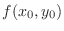 is a local minimum.
is a local minimum.
| Check |
|---|
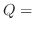 positive positive positive positive![$+\frac{(\mbox{positive})\mbox{positive}}{\mbox{positive}}\big]$](img713.png) . Thus . Thus 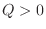 . .
|
2. If
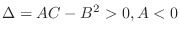 , then since
, then since  is the class
is the class 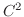 func, for any
func, for any 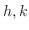 such that
such that 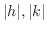 is sufficiently small and never 0 simulteneously, we have
is sufficiently small and never 0 simulteneously, we have 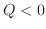 . Thus
. Thus
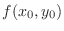 is a local maximum.
is a local maximum.
| Check |
|---|
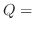 negative negative positive positive![$+\frac{(\mbox{positive})\mbox{positive}}{\mbox{positive}}\big]$](img713.png) . Thus . Thus 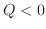 . .
|
3. If
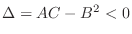 and
and 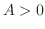 , then
, then 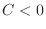 which gives a saddle point. Similarly, if
which gives a saddle point. Similarly, if
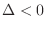 and
and 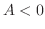 , then
, then 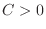 which give a saddle point.
which give a saddle point.

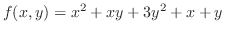
SOLUTION In Example4.16, we found the critical point. Now we check to see whether the function takes a local extremum at the critical point. Now by the 2nd derivative test,
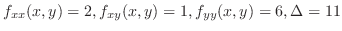
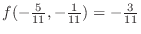 is a local minimum.
is a local minimum.

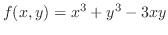
| Check |
|---|
Multiply the equation 4.1 by 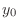 and multiply the equation 4.2 by and multiply the equation 4.2 by 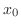 . Then subtract the latter one from the former one to obtain . Then subtract the latter one from the former one to obtain
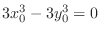 . From this, we get . From this, we get 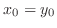 and put this back to the equation 4.1, then and put this back to the equation 4.1, then
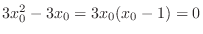 . Thus, . Thus, 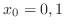 . .
|
SOLUTION Let
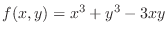 . Then we have
. Then we have
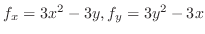 .
If
.
If  takes the local maxima at
takes the local maxima at
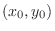 , then
, then
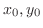 . Then substitute the equation
. Then substitute the equation
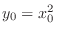 , which is derived from the equation 4.1, to the equation 4.2. Then
, which is derived from the equation 4.1, to the equation 4.2. Then
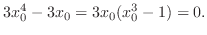
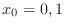 . Hence,
. Hence,
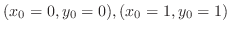 .
.
Now we apply the 2nd derivative test.
Since
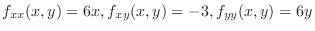 , at
, at 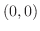 we have
we have
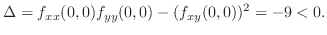
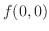 is not extrema.
Now at
is not extrema.
Now at 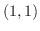 , we have
, we have
 |
 |
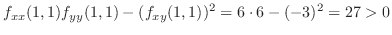 |
|
 |
 |
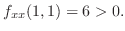 |
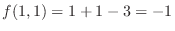 is the local minimum
is the local minimum

 at
at  .D
.D
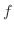 at
at 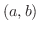 D
D