Next: Taylor Theorem for Two Up: Partial Differentiation Previous: Higher Order Partial Derivatives Contents Index
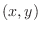 in the
in the 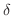 neighborhood of
neighborhood of 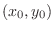 4.1
4.1
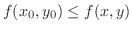 , then
, then  takes minimum at
takes minimum at
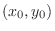 and
and
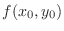 is called local minimum of
is called local minimum of  .
.
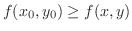 , then
, then  takes maximum at
takes maximum at
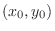 and
and
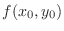 is called local maximum of
is called local maximum of  .
. NOTE A locam minimum and a local maximum togrther are called extrema.
If the graph of function is smooth, then
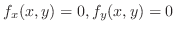 .
.
If the graph has a sharp edge, then the function is not differentiable at the sharp edge.
 has a extremum at
has a extremum at
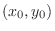 , then .
, then .
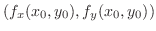 exists and
exists and
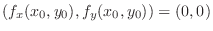 , or
, or
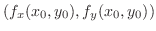 does not exist.
does not exist.
Proof
Since
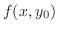 takes a extreme value at
takes a extreme value at 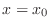 ,
,
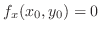 or
or
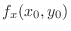 does not exist. Similarly for
does not exist. Similarly for 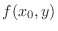 .
.
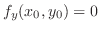 or
or
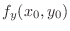 does not exist
does not exist

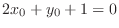 implies
implies
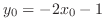 . substitute this inot
. substitute this inot
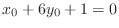 to get
to get
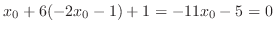 . Thus,
. Thus,
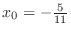 .
.
SOLUTION
If  takes the extreme value at
takes the extreme value at
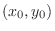 , then
, then
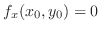 implies
implies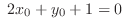
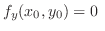 implies
implies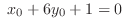
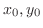 . Then
. Then
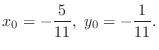
 may takes the extreme value at
may takes the extreme value at
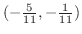 . Now we have to check to see if this is a local maximum or minimum.owari
. Now we have to check to see if this is a local maximum or minimum.owari
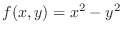
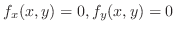 is not sufficient condition for the existence of a limit.
is not sufficient condition for the existence of a limit.
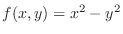 . Find
. Find 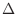 at
at 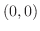 . Then
. Then
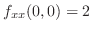 ,
,
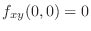 ,
,
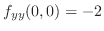 . Thus,
. Thus,
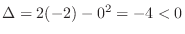 and
and 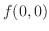 is not extreme value.
is not extreme value.
SOLUTION If  takes the extreme value at
takes the extreme value at
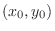 , then
, then
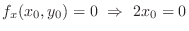
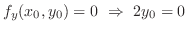
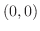 is a critical point. Now as
is a critical point. Now as 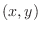 approaches
approaches 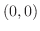 along
along  -axis, we have
-axis, we have
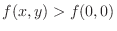 , along
, along  -axis we have
-axis we have
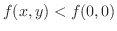 . Thus
. Thus 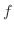 does not take the extreme value at
does not take the extreme value at 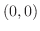

 be the class
be the class 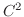 at
at 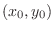 in the region
in the region 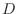 . If
. If
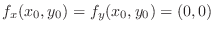 , then denote
, then denote
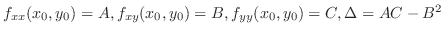 .
.
1. If
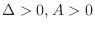 , then
, then
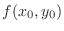 is a local minimum.
is a local minimum.
2. If
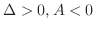 , then
, then
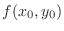 is a local maximum.
is a local maximum.
3. If
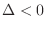 , then
, then
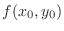 is a saddle point
is a saddle point
4. If
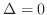 , then test is no conclusive.
, then test is no conclusive.
| Check |
|---|
For
![$Q = \frac{A}{2}\left[(h + \frac{Bk}{A})^2 + \frac{(AC - B^2)k^2}{A^2}\right]$](img638.png) , ,
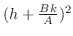 and and
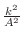 are squares and thus non negative. Therefore, the sign of are squares and thus non negative. Therefore, the sign of 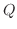 is determined by the sign of is determined by the sign of 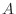 and and 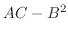 . .
|