Next: Continous functions Up: Limit of Functions Previous: Limit of Functions Contents Index
 approaches
approaches 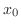 with the restriction
with the restriction 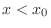 ,
,  is always smaller than
is always smaller than 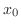 . Then we write
. Then we write
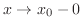 or
or
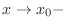 . Similarly, if
. Similarly, if  appraoches
appraoches 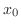 taking larger value than
taking larger value than 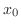 , then we write
, then we write
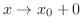 or
or
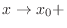 .
.
Left-hand limit
If  approaches
approaches 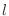 as
as
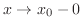 , then we write
, then we write
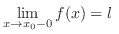 or
or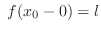
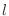 , left-hand limit.
, left-hand limit.
Right-hand limit
If  approaches
approaches 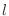 as
as
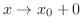 , then we write
, then we write
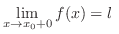 or
or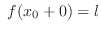
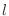 , right-hand limit
, right-hand limit
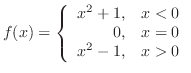
 approaches 0 fram the left,
approaches 0 fram the left,  is always smaller than 0. Thus
is always smaller than 0. Thus 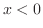 and
and
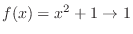 . Therefore,
. Therefore,
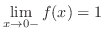
 approaches 0 from the right, then
approaches 0 from the right, then  is always larger than 0. Thus
is always larger than 0. Thus 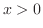 and
and
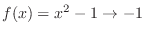 . Therefore,
. Therefore,
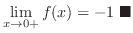
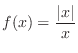 at 0.
at 0.
SOLUTION Note that for 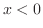 we have
we have 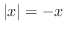 .
.
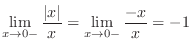
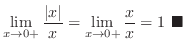
Existence of a limit
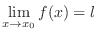 iff
iff
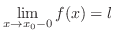 and
and
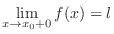 .
.
Non-existence of a limit To show non-existence of a limit, it is enough to show
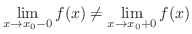 .
.
NOTE The existence of
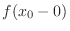 and the existence of
and the existence of
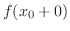 , and equality of their values is suffice to say the existence of a limit of
, and equality of their values is suffice to say the existence of a limit of  . Otherwise, no limit exists.
. Otherwise, no limit exists.
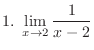
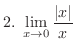
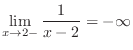
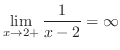

Check to see the existence of the right-hand limit and left-hand limit.
2. Since the right-hand limit is not equql to the left-hand limit, by Exercise![[*]](crossref.png) , we have
, we have
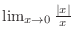

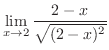 .
.
Recall that
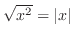 . Note that
. Note that 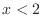 implies
implies 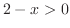 which in turn implies
which in turn implies
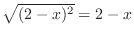 . Note also that
. Note also that 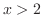 implies
implies 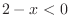 which in turn implies
which in turn implies
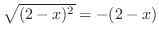 .
.
SOLUTION
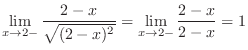
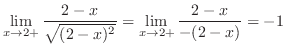

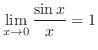 , find the limit of the following functions:
, find the limit of the following functions:
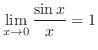 , find the limit of the followings:
, find the limit of the followings:
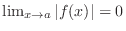 implies
implies
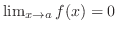 .
.