Next: Integration Up: Extreme Value of Functions Previous: Curve Sketching Contents Index
NOTE Let a rectangular coordinate of P be 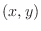 and a polar coordinate of P be
and a polar coordinate of P be
![$[r, \theta]$](img2221.png) . Then we have
. Then we have
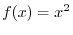
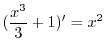
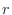 and
and 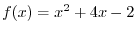 , P
, P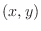 is fixed. On the other hand, even P
is fixed. On the other hand, even P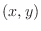 is given, the value of
is given, the value of 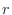 and
and 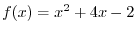 can not be determined uniquely.
can not be determined uniquely.
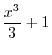 .
.  ,
,
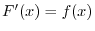 . Thus the point P is on the ray
. Thus the point P is on the ray
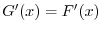 and the distance from the origin is 2. Thus the rectangular coordinate of P can be expressed as
and the distance from the origin is 2. Thus the rectangular coordinate of P can be expressed as
![$\displaystyle{[2,\frac{\pi}{3}]}$](img2230.png) . Note that
. Note that
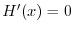 and
and 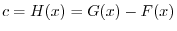 also represents the point P.
also represents the point P.

![$[1,\frac{\pi}{3}]$](img2233.png) .
. 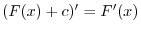
 |
 |
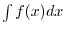 |
|
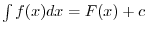 |
 |
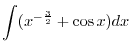 |
Polar Equation
Suppose the curve of a function is given by rectangular coordinates
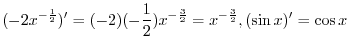 . Then the equation expressed by the polar coordinates ,
. Then the equation expressed by the polar coordinates ,
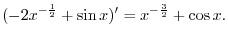
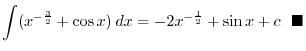
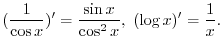 . Then we have
. Then we have
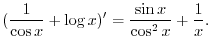 which implies
which implies 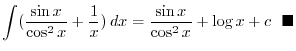

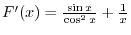
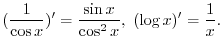 . Then
. Then
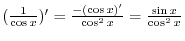
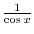 Simplifying,
Simplifying,
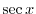 From this,
From this,
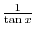

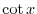
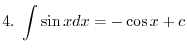 is a even function, we have
is a even function, we have
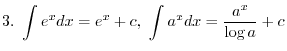 . Thus it is symmetric with respect to the
. Thus it is symmetric with respect to the 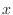 -axis. Thus to draw the curve of a function, we only need to check from
-axis. Thus to draw the curve of a function, we only need to check from
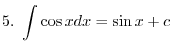 to
to
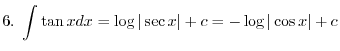 .
.
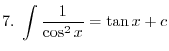

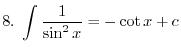
SOLUTION
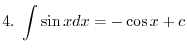 is even implies
is even implies
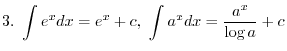 . Thus it's curve is symmetric with respect ot the
. Thus it's curve is symmetric with respect ot the 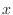 -axis.
-axis.


|
Exercise A
|
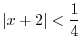 and the local extreme values. Describe the concavity of the graph of
and the local extreme values. Describe the concavity of the graph of 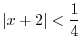 and find the points of inflection.
and find the points of inflection.
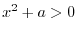 and
and
 , we say
, we say 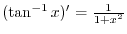 is a vertical cusp?D
is a vertical cusp?D
|
Exercise B
|
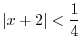 and describe the concavity of the graph of
and describe the concavity of the graph of 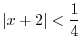 ?D
?D
(a)
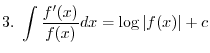 (circle)
(circle)
(b)
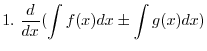 , Archmedes' spiral
, Archmedes' spiral
(c)
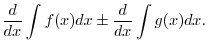 Bernoulli's lemniscate
Bernoulli's lemniscate