Next: Curve Sketching Up: Differentiation Previous: Taylor's Theorem Contents Index
| Extreme Value |
|---|
For all 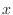 in the neighborhood of in the neighborhood of  , ,
 . Then we say . Then we say 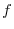 takes local maximum at takes local maximum at 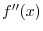 . if . if
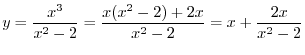 , then we say , then we say 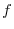 takes local minimum at takes local minimum at 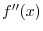 . local maximum and local minimum together called local extrema. . local maximum and local minimum together called local extrema.
|
| First Derivative Test |
|---|
|
Theorem 2..18 Suppose that
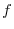 is differentiable at is differentiable at 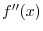 . If . If 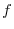 takes local extrema at takes local extrema at 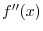 , then , then
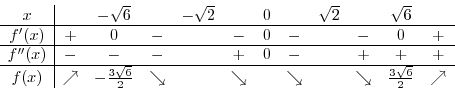 . . |
NOTE
If
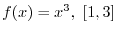 , then
, then 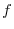 is increasing at
is increasing at 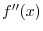 . If
. If
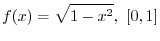 , then
, then  is decreasing at
is decreasing at 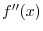 . In these cases,
. In these cases, 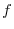 does not take local extrema. Thus we must have
does not take local extrema. Thus we must have
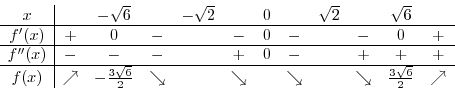 .
.
| Criterion for Local Extrema | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Theorem 2..19 Suppose that
 is continuous on a neighborhood of is continuous on a neighborhood of  . If . If 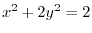 is small enough, then is small enough, then
|
NOTE
1. 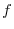 is strictly increasing function on
is strictly increasing function on ![$[a-h,a]$](img2171.png) and strictly decreasin on
and strictly decreasin on ![$[a,a+h]$](img2172.png) . Thus
. Thus 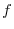 takes the local maximum at
takes the local maximum at 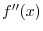 .
.
If
If
If
NOTE Apply the above theorem to a function
2nd Derivative Test
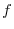 is twice differentialbe on a interval containing
is twice differentialbe on a interval containing 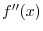 and satisfies
and satisfies
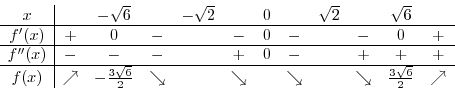 .
.
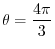 , then the graph of
, then the graph of 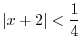 is concave up, and
is concave up, and 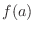 is local minimum
is local minimum
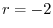 , then the graph of
, then the graph of 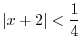 is concave down, and
is concave down, and 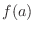 is local maximum
is local maximum
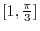 and concavity changes, then
and concavity changes, then 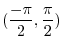 is an inflection point.
is an inflection point. 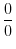 , Then
, Then
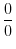 is increasing at
is increasing at 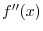 . Since
. Since
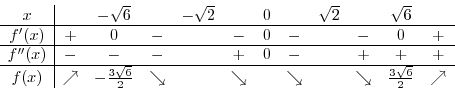 ,
,
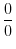 takes negative on
takes negative on
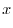 on positive on
on positive on
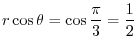 . Thus the graph of a function is concave up at
. Thus the graph of a function is concave up at 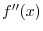 and takes a local minimum at
and takes a local minimum at 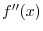 .
.
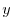 and concavity of the graph of
and concavity of the graph of 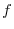 .
.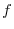 is differentiable on
is differentiable on
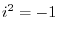 , if
, if 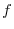 attains etremumat some point, then at the point
attains etremumat some point, then at the point
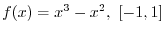 . Thus, we find
. Thus, we find 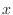 so that
so that
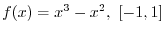 . Since
. Since
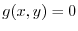
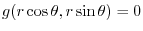 are the candidate for critical point. Next to check concavity of the graph of
are the candidate for critical point. Next to check concavity of the graph of 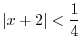 , we find
, we find
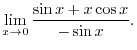 . Since
. Since
 are the candidate for inflection point.
Now we create a concavity table.
are the candidate for inflection point.
Now we create a concavity table.
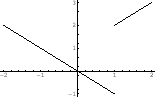
 is a local maximum.
is a local maximum.
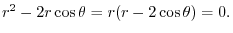 is a local minimum. By the 2nd derivative test,
is a local minimum. By the 2nd derivative test, 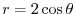 is an inflection point. The graph of function is concave down on the left-hand side of the inflection point and concave up on the right-hand side of the inflection point
is an inflection point. The graph of function is concave down on the left-hand side of the inflection point and concave up on the right-hand side of the inflection point

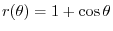 and concavity of the graph of
and concavity of the graph of  .
.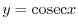 |
 |
 |
|
 |
 |
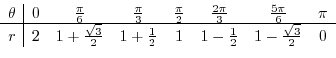 |
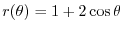 are candidates for a critical point. Now write a concavity table.
are candidates for a critical point. Now write a concavity table.