Next: Partial derivatives Up: PARTIAL DIFFERENTIATION Previous: Limit of function 索引
6.2
1.
(a)
 represents a unit circle and does not contain the center and the perimeter. Thus, take any point in
represents a unit circle and does not contain the center and the perimeter. Thus, take any point in  , the neighborhood can be included in
, the neighborhood can be included in  .Thus,
.Thus, is open set.
is open set.
 is included in the circle with the radius
is included in the circle with the radius  . Thus, bounded.
. Thus, bounded.
Any two points in  are connected by a continuous curve inside of
are connected by a continuous curve inside of  . Thus, connected.
. Thus, connected.
A connected open set is called a region. Thus  is region.
is region.
The boundary of  is
is

The closure of  is
is

Since
 , we have
, we have
 .Now
.Now  is open set. Thus
is open set. Thus  is closed set.
is closed set.
For any open disk
 ,
,  is not included. Thus unbounded.
is not included. Thus unbounded.
Any two point in  can be connected by continuous curve inside of
can be connected by continuous curve inside of  . Thus
. Thus  is connected.
is connected.
The boundary of  is
is

The closure of  is
is

2.
(a)
The least degree in the numerator  the least degree in the denominator
the least degree in the denominator  .Thus, as
.Thus, as 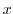 goes to 0, the denominator goes to 0 faster than the numerator.So, we let
goes to 0, the denominator goes to 0 faster than the numerator.So, we let  . Then
. Then

(b)
The least degree in the numerator  the least degree in the denominator
the least degree in the denominator  . Thus we let
. Thus we let  . Then
. Then

 . Thus,
. Thus,
 does not exist.
(c)
The least degree in the numerator
does not exist.
(c)
The least degree in the numerator  the least degree in the denominator
the least degree in the denominator  . Thus, we let
. Thus, we let
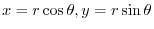 . Then
. Then

 .
.
3.

The least degree in the numerator  the least degree in the denominator
the least degree in the denominator  .Thus the numerator goes to 0 faster than the denominator.Now let
.Thus the numerator goes to 0 faster than the denominator.Now let
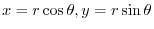 . Then
. Then

 and
and 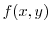 is continuous at
is continuous at 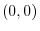 .
.
(b)
The least degree in the numerator  the least degree in the denominator
the least degree in the denominator  . Then we let
. Then we let  .
.

 . Thus,
. Thus,
 does not exist.Therefore,
does not exist.Therefore, 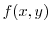 is dicontinuous at
is dicontinuous at 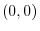 .
.
(c)
When 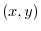 approaches
approaches 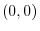 ,the speed of approaching 0 is faster than the
,the speed of approaching 0 is faster than the
 approaches
approaches  . Then let
. Then let
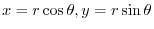 .
.

 and
and 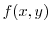 is discontinuous at
is discontinuous at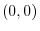 .
.