Next: Limit of function Up: PARTIAL DIFFERENTIATION Previous: Definition of functions 索引
6.1
1.
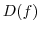 |
 |
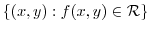 |
|
 |
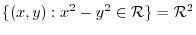 |
Let 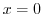 . Then
. Then
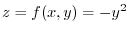 . Thus, a parabola on
. Thus, a parabola on 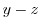 plane.
Let
plane.
Let 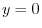 . Then
. Then
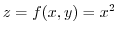 . Thus a parabola on
. Thus a parabola on  plane.
Let
plane.
Let 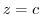 . Then
. Then
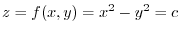 . Thus, a hyperbola on the plane
. Thus, a hyperbola on the plane 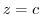 .
.
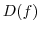 |
 |
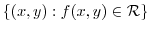 |
|
 |
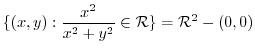 |
Let 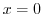 . Then
. Then
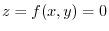 .
Let
.
Let 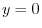 . Then
. Then
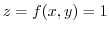 . Thus a line on
. Thus a line on  plane.
Let
plane.
Let 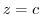 . Then
. Then
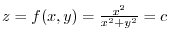 . Thus
. Thus
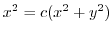 .
.
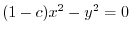 and
and
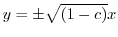
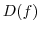 |
 |
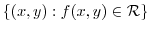 |
|
 |
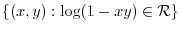 |
||
 |
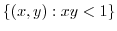 |
Let 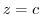 . Then
. Then
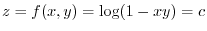 . Thus
. Thus
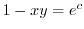 .
.
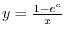 .Now changing the value of
.Now changing the value of 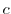 , draw a graph.
, draw a graph.