Next: Extreme values Up: PARTIAL DIFFERENTIATION Previous: Differentiation of composite functions 索引
6.6
1.
![\begin{figure}\begin{center}
\includegraphics[width=6cm]{CALCFIG/Fig6-6-2.eps}
\end{center}\end{figure}](img234.png)
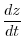 |
 |
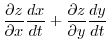 |
|
 |
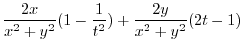 |
Let
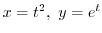 . Then
. Then
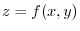 .
.
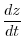 |
 |
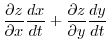 |
|
 |
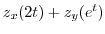 |
Let
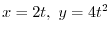 . Then
. Then
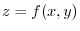 .
.
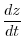 |
 |
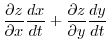 |
|
 |
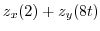 |
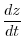 |
 |
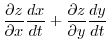 |
|
 |
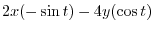 |
2.
![\begin{figure}\begin{center}
\includegraphics[width=6cm]{CALCFIG/Fig6-6-1.eps}
\end{center}\end{figure}](img244.png)
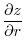 |
 |
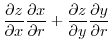 |
|
 |
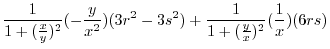 |
||
 |
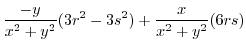 |
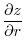 |
 |
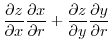 |
|
 |
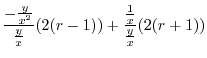 |
||
 |
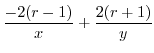 |
||
 |
 |
 |
 |
 |
|
 |
 |
||
 |
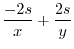 |
||
 |
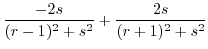 |
3.
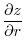 |
 |
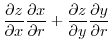 |
|
 |
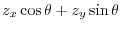 |
||
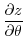 |
 |
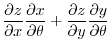 |
|
 |
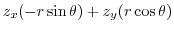 |
||
 |
 |