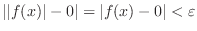Next: Right-hand limit, Left-hand limit Up: FUNCTIONS Previous: Limit of function
1.3
1.
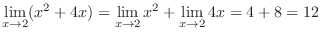
(b)
As 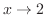 ,both
,both
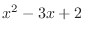 and
and 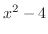 approach to 0. Thus,
approach to 0. Thus,
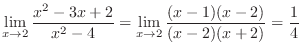
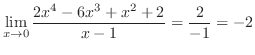
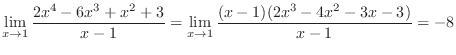
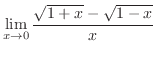 |
 |
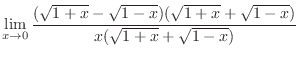 |
|
 |
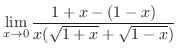 |
||
 |
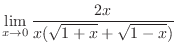 |
||
 |
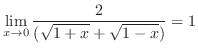 |
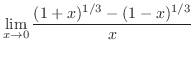 |
 |
![$\displaystyle \lim_{x \rightarrow 0}\frac{(1+x) - (1 - x)}{x[(1+x)^{2/3} + (1+x)^{1/3}(1-x)^{1/3} + (1-x)^{2/3}]}$](img163.png) |
|
 |
![$\displaystyle \lim_{x \rightarrow 0}\frac{2x}{x[(1+x)^{2/3} + (1+x)^{1/3}(1-x)^{1/3} + (1-x)^{2/3}]}$](img164.png) |
||
 |
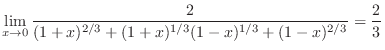 |
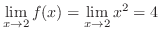
2.
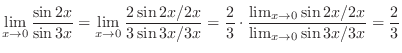
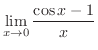 |
 |
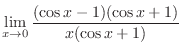 |
|
 |
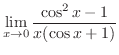 |
||
 |
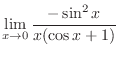 |
||
 |
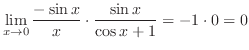 |
Alternate solution
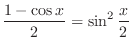 を用いると
を用いると
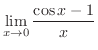 |
 |
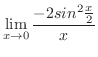 |
|
 |
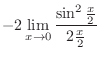 |
||
 |
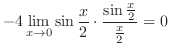 |
(c)
Let
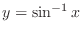 . Then
. Then
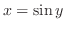 .Also,for
.Also,for 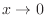 ,
,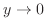 .Thus,
.Thus,
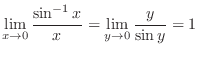
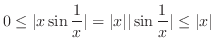
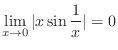
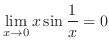
Note that
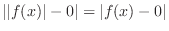 .For all
.For all
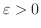 ,there exists
,there exists 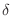 such that for
such that for
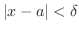 , then
, then