Next: Evaluation of definite integrals Up: INTEGRATION Previous: Definite integral
3.7
1.
Note that by fundamental theorem of calculus, if 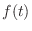 is continuous on
is continuous on ![$[a,b]$](img1285.png) , then for
, then for 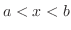 ,
,
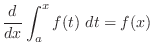
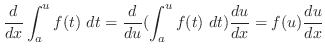
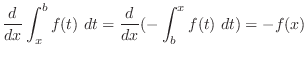
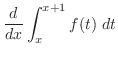 |
 |
![$\displaystyle \frac{d}{dx}[\int_{x}^{a}f(t)\ dt + \int_{a}^{x+1}f(t)\ dt]$](img1291.png) |
|
 |
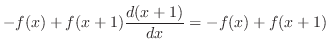 |
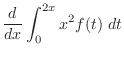 |
 |
 |
|
 |
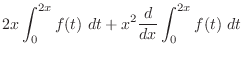 |
||
 |
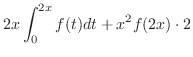 |
2.
(a) Let
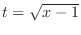 . Then
. Then 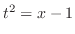 and
and 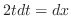 DThen note that
DThen note that
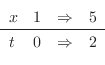
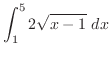 |
 |
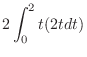 |
|
 |
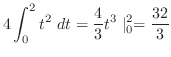 |
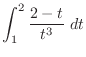 |
 |
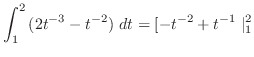 |
|
 |
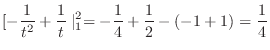 |
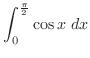 |
 |
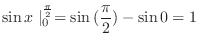 |
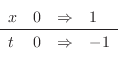
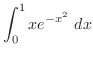 |
 |
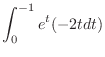 |
|
 |
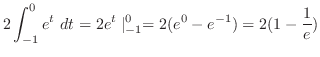 |
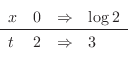
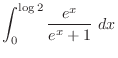 |
 |
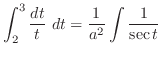 |
|
 |
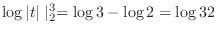 |
3.
4.
(a) For 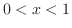 and
and 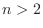 , we evaluate
, we evaluate 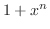 .
First
.
First
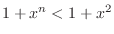 implies that
implies that
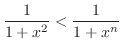
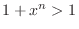 implies
implies
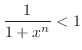
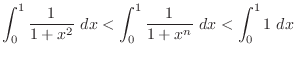
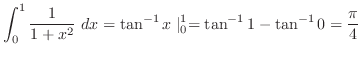
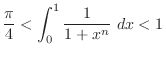
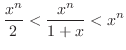
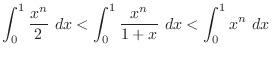
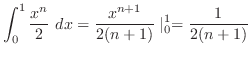
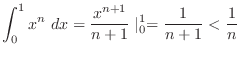
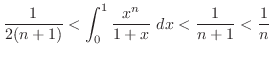
5.
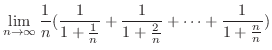 |
 |
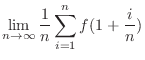 |
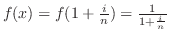 implies
implies
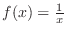 . Thus,
. Thus,
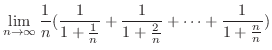 |
 |
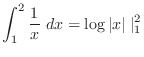 |
|
 |
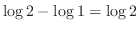 |
Alternate solution
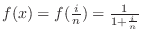 implies
implies
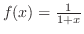 . Then
. Then
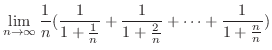 |
 |
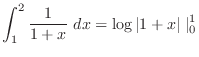 |
|
 |
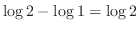 |
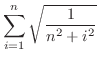 |
 |
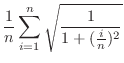 |
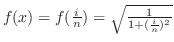 implies
implies
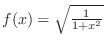 . Then
. Then
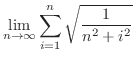 |
 |
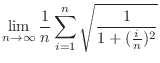 |
|
 |
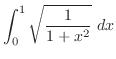 |
||
 |
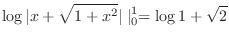 |
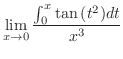 |
 |
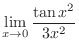 |
|
 |
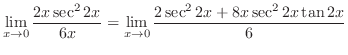 |
||
 |
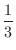 |