Next: Definite integral Up: INTEGRATION Previous: Integration of irrational functions
3.6
1.
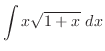 |
 |
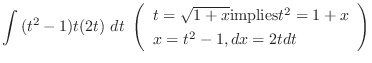 |
|
 |
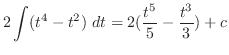 |
||
 |
![$\displaystyle 2[\frac{(1 + x)^{5/2}}{5} - \frac{(1+x)^{3/2}}{3}] + c$](img1061.png) |
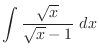 |
 |
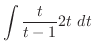 |
|
 |
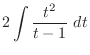 |
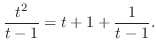
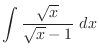 |
 |
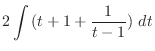 |
|
 |
![$\displaystyle 2[\frac{t^2}{2} + t + \log{\vert t-1\vert}] + c$](img1070.png) |
||
 |
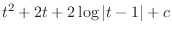 |
||
 |
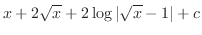 |
(c) Let
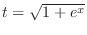 . Then
. Then
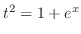 and
and
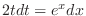 .Now express the integrand interms ot
.Now express the integrand interms ot 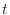 and
and 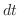 . Then
. Then
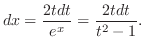
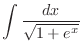 |
 |
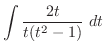 |
|
 |
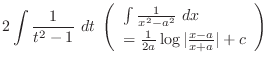 |
||
 |
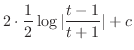 |
||
 |
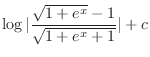 |
(d) Let
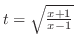 . Then
. Then
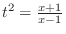 . To find
. To find 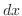 , rewrite the above equation in
, rewrite the above equation in  and solve for
and solve for  .
.
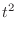 |
 |
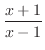 |
|
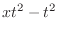 |
 |
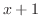 |
|
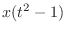 |
 |
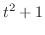 |
|
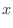 |
 |
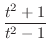 |
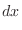 |
 |
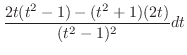 |
|
 |
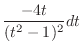 |
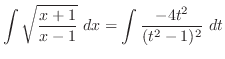
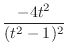 |
 |
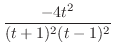 |
|
 |
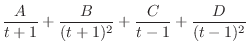 |
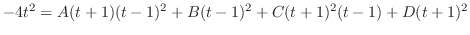
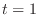 . Then
. Then
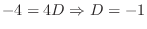
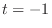 . Then
. Then
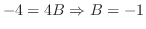
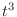 . Then
. Then
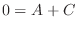
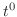 . Then
. Then
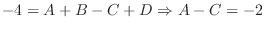
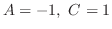
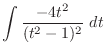 |
 |
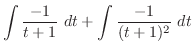 |
|
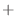 |
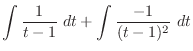 |
||
 |
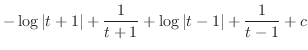 |
||
 |
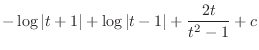 |
||
 |
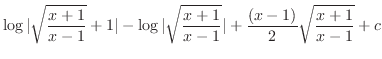 |
2.
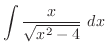 |
 |
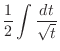 |
|
 |
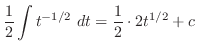 |
||
 |
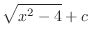 |
(b) Let
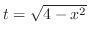 . Then
. Then
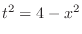 implies
implies
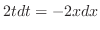 . Now consider the traiangle with the angle
. Now consider the traiangle with the angle 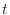 and whose opposite side is
and whose opposite side is  and whose hypotenuse is 2. Then the bottom is
and whose hypotenuse is 2. Then the bottom is
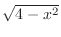 .Now let
.Now let
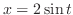 . Then
. Then
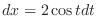 and
and
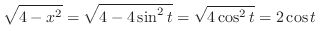
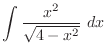 |
 |
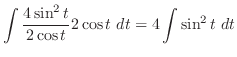 |
|
 |
![$\displaystyle 4\int{\frac{1 - \cos{2t}}{2}}\ dt = 2[t - \frac{\sin{2t}{2}}] + c$](img1127.png) |
||
 |
![$\displaystyle 2[t - \sin{t}\cos{t}] + c = 2[\sqrt{4 - x^2} - \frac{x}{2}\frac{\sqrt{4 - x^2}}{2} + c$](img1128.png) |
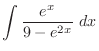 |
 |
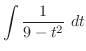 |
|
 |
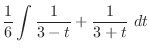 |
||
 |
![$\displaystyle \frac{1}{6}[-\log\vert 3-t\vert + \log\vert 3 + t\vert] +c = \frac{1}{6}\log\vert\frac{3+t}{3-t}\vert + c$](img1132.png) |
||
 |
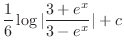 |
(d) Let
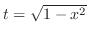 . Then
. Then
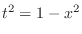 and
and
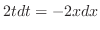 . Now consider the triangle with the angle
. Now consider the triangle with the angle 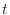 and whose opposite side is
and whose opposite side is  and thee hypotenuse is 1. Then the bottom is
and thee hypotenuse is 1. Then the bottom is
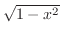 . Now
. Now
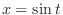 implies
implies
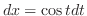 and ,
and ,
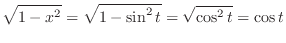
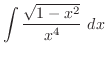 |
 |
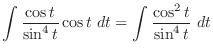 |
Let
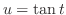 . Then
. Then
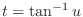 and
and
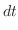 |
 |
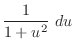 |
|
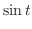 |
 |
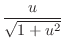 |
|
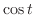 |
 |
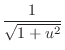 |
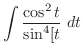 |
 |
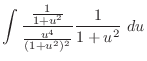 |
|
 |
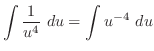 |
||
 |
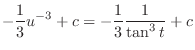 |
||
 |
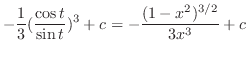 |
(e) Let
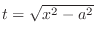 と. Then
と. Then
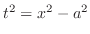 and
and
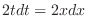 . Now consider the triangle with the angle
. Now consider the triangle with the angle 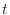 and whose hypotenuse is
and whose hypotenuse is  and the bottom is
and the bottom is 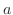 . Then we have the opposite side is
. Then we have the opposite side is
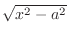 .Then
.Then
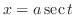 implies
implies
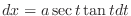 and
and
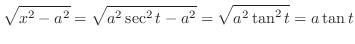
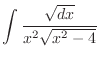 |
 |
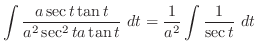 |
|
 |
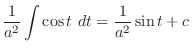 |
||
 |
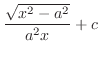 |
(f) Let
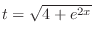 . Then
. Then
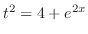 and
and
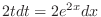 . Consider the triangle with the angle
. Consider the triangle with the angle 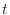 and whose opposite side is
and whose opposite side is 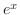 and the bottom is 2. Then the hypotenuse is
and the bottom is 2. Then the hypotenuse is
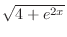 .Now
.Now
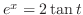 and
and
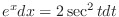 .Also, ,
.Also, ,
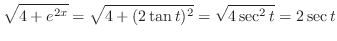
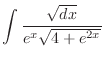 |
 |
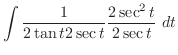 |
|
 |
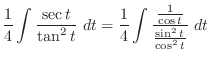 |
||
 |
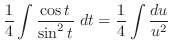 |
||
 |
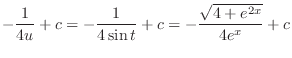 |
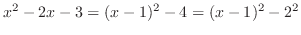
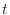 and whose hypotenuse is
and whose hypotenuse is 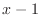 and the bottom is
and the bottom is 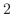 . Then the opposite side is
. Then the opposite side is
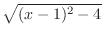 . Now
. Now
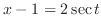 implies
implies
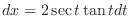 and
and
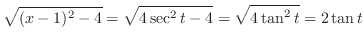
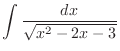 |
 |
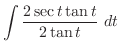 |
|
 |
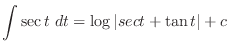 |
||
 |
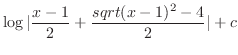 |
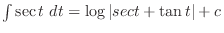 . Without the formula, we can integrate the following way.
. Without the formula, we can integrate the following way.
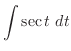 |
 |
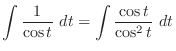 |
|
 |
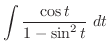 |
||
 |
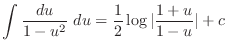 |
||
 |
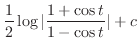 |
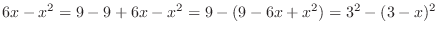
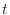 and whose hypotenuse is
and whose hypotenuse is 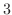 ,the bottom is
,the bottom is
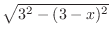 ,the height is
,the height is 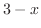 . Then
. Then
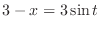 implies
implies
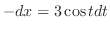 and
and
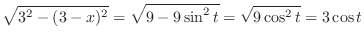
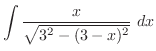 |
 |
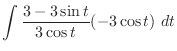 |
|
 |
![$\displaystyle -\int{3 - 3\sin{t}}\ dt = -[3t + 3\cos{t}] + c$](img1206.png) |
||
 |
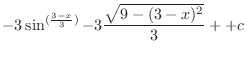 |
||
 |
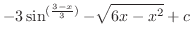 |
(i) Completing the square, we have
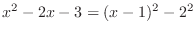
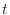 and whose hypotenuse is
and whose hypotenuse is 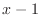 ,the bottom is
,the bottom is 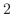 ,the height is
,the height is
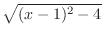 . Then
. Then
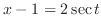 implies
implies
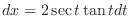 and
and
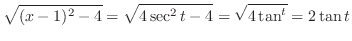
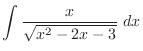 |
 |
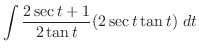 |
|
 |
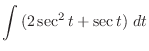 |
||
 |
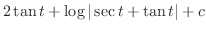 |
||
 |
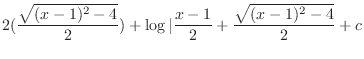 |
||
 |
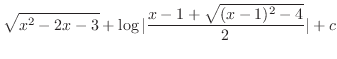 |
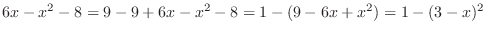
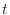 and whose hypotenuse is
and whose hypotenuse is 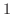 ,the bottom is
,the bottom is
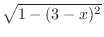 ,and the height is
,and the height is 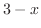 . Then
. Then
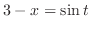 implies
implies
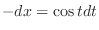 and,
and,
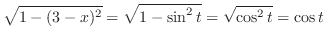
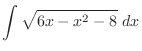 |
 |
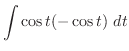 |
|
 |
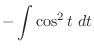 |
||
 |
![$\displaystyle -\int{\frac{1 + \cos{t}}{2}}\ dt = -[\frac{t}{2} + \frac{\sin{2t}}{4}] + c$](img1226.png) |
||
 |
![$\displaystyle -[\frac{t}{2} + \frac{\sin{t}\cos{t}}{2}] + c$](img1227.png) |
||
 |
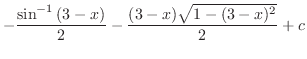 |
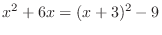
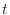 and whose hypotenuse is
and whose hypotenuse is 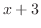 ,the bottom is
,the bottom is 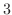 ,and the height is
,and the height is
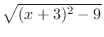 . Then
. Then
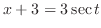 implies
implies
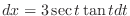 and
and
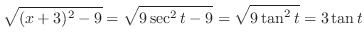
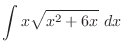 |
 |
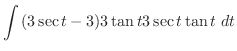 |
|
 |
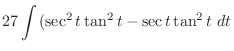 |
||
 |
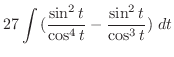 |
Now integrate
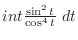 .
In this case, the degree of the numerator and the denominator is even. So, we let
.
In this case, the degree of the numerator and the denominator is even. So, we let
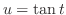 . Then
. Then
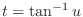 and
and
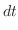 |
 |
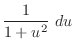 |
|
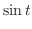 |
 |
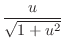 |
|
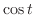 |
 |
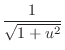 |
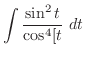 |
 |
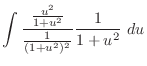 |
|
 |
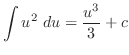 |
||
 |
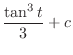 |
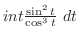 .In this case the degree of the denominator is odd. Then we multiply
.In this case the degree of the denominator is odd. Then we multiply 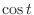 to both the numerator and the denominator. Then we have
to both the numerator and the denominator. Then we have
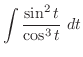 |
 |
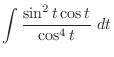 |
|
 |
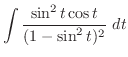 |
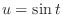 , Then
, Then
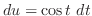 and
and
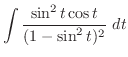 |
 |
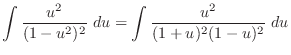 |
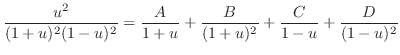
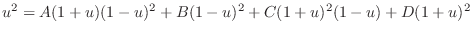
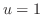 . Then
. Then
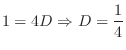
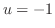 . Then
. Then
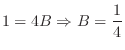
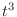 . Then
. Then
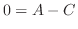
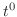 . Then
. Then
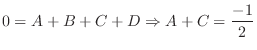
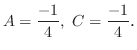
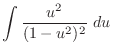 |
 |
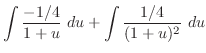 |
|
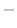 |
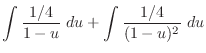 |
||
 |
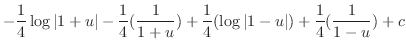 |
||
 |
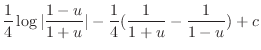 |
||
 |
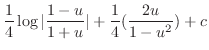 |
||
 |
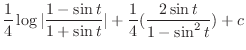 |
Therefore,
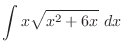 |
 |
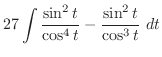 |
|
 |
![$\displaystyle 27[\frac{\tan^{3}{t}}{3} + \frac{1}{4}\log\vert\frac{1-\sin{t}}{1+\sin{t}}\vert + \frac{1}{4}(\frac{2\sin{t}}{1-\sin^{2}{t}}) ]+ c$](img1269.png) |
||
 |
![$\displaystyle 27[\frac{1}{3}(\frac{\sqrt{x^2 + 6x}}{3})^{3} + \frac{1}{4}\log\v...
...(\frac{2\frac{\sqrt{x^2 + 6x}}{x+3}}{1-(\frac{\sqrt{x^2 + 6x}}{x+3})^{2}})] + c$](img1270.png) |