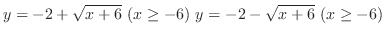Next: elementary functions Up: FUNCTIONS Previous: Definition of function
1.1
1.
(a) For example, conside the case 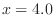 . Then the
. Then the 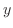 satisfying
satisfying
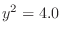 are given by
are given by
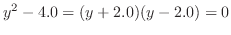
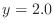 or
or 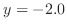 .Then,
.Then,
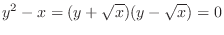
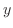 satisfying
satisfying
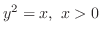 are
are
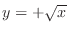 and
and
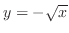 .Therefore,for different
.Therefore,for different  ,there are 2
,there are 2 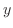 corresopobds to it. Thus, double valued function.
corresopobds to it. Thus, double valued function.
(b) For example,consider
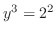 . Then
. Then
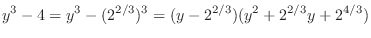
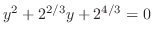 is a quadratic equation in
is a quadratic equation in 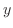 . So, we use the discriminant. Then
. So, we use the discriminant. Then
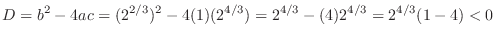
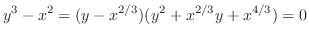
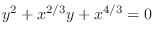 has no real root. Then
has no real root. Then
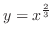 is the only real root.Therefore, single valued function.
is the only real root.Therefore, single valued function.
2.
(a) The domain of f(x) is the set of real numbers of  such that
such that 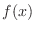 is real. Then
is real. Then
![$D(f) = [-2,2]$](img31.png) .
.
(b) The domain of f(x) is the set of real numbers of  such that
such that 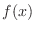 is real. Then
is real. Then
![$\displaystyle{D(h) = (-\infty,-\frac{1}{2}) \cup (0, \frac{4}{3}]}$](img32.png)
3.
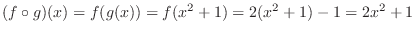
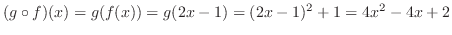
(b) 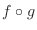 cna be defined if the range of
cna be defined if the range of 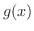 is in the domain of
is in the domain of 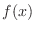 .So, we check the range of
.So, we check the range of 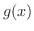 .
.
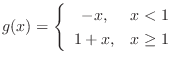
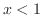 ,
,
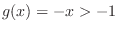 .Thus the the range of
.Thus the the range of 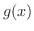 is contained in the domain of
is contained in the domain of 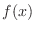 . Now we divide the case
. Now we divide the case 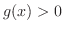 and
and
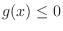 .
.
For 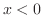 ,
,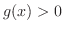 and for
and for
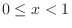 ,
,
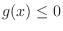 .Thus,
for
.Thus,
for 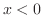 ,we use
,we use
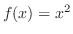 and for
and for
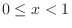 ,ew use
,ew use
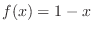 . Therefore,
. Therefore,
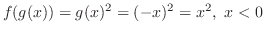
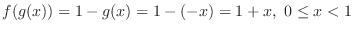
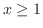 ,
,
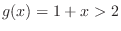 .This is in the domain of
.This is in the domain of 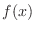 . Thus we use
. Thus we use
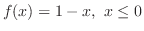 .Therefore,
.Therefore,
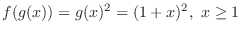
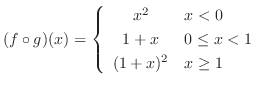
Similarly, ,
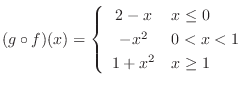
4.
(a) First we show that this function is oe-to-one.
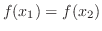 |
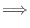 |
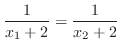 |
|
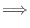 |
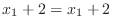 |
||
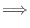 |
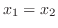 |
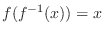 to find the inverse.
to find the inverse.
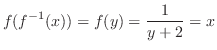
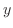 . Then
. Then
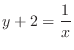 .Therefore,
.Therefore,
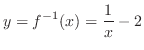 .
.
(b) This function is not one-to-one. Since
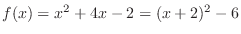 ,it is symmetric about
,it is symmetric about  -axis.Thus, there is no inverse function. But we can restrict the domain of
-axis.Thus, there is no inverse function. But we can restrict the domain of  so that it is one-to-one. For if we write the domain as
so that it is one-to-one. For if we write the domain as
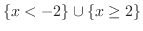 , then on this domain, we can find the inverse.
, then on this domain, we can find the inverse.
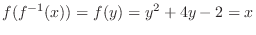
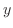 . Then we have
. Then we have