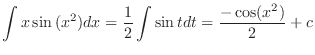Next: Integration by parts Up: INTEGRATION Previous: Integration by substitution
3.2
1.
(a) Let 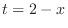 . Then
. Then
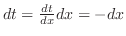 . Thus, the given integral is a function of
. Thus, the given integral is a function of 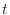 and
and 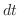 . Thus,
. Thus,
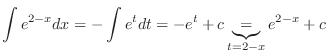
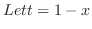 . Then
. Then 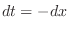 . Thu, we can express as a function of
. Thu, we can express as a function of 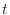 ,
,
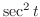 . Thus,
. Thus,
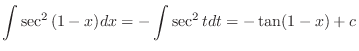
Let
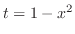 . Then
. Then
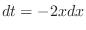 and
and
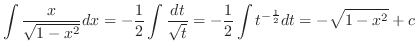
Let
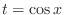 . Then
. Then
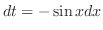 and
and
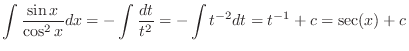
Let
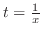 . Then
. Then
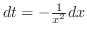 and
and
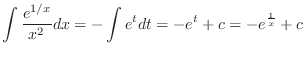
Let
 . Then
. Then
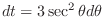 and
and
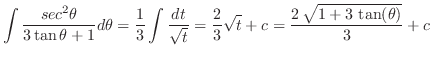
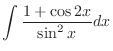 |
 |
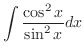 |
|
 |
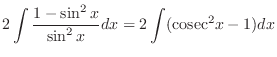 |
||
 |
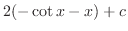 |
Let
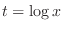 . Then
. Then
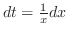 and
and
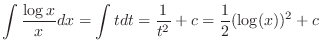
Let 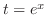 . Then
. Then
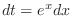 and
and
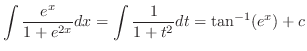
Let 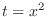 . Then
. Then
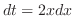 and
and