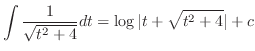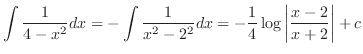3.1 Answer

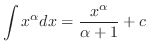(a) Note that the integration formula $\displaystyle{\int x^{\alpha}dx = \frac{x^{\alpha}}{\alpha + 1} + c}$ .

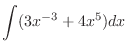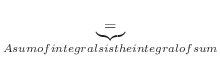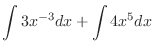$\displaystyle \int (3x^{-3} + 4x^{5}) dx$	$\displaystyle \underbrace{=}_{A sum of integrals is the integral of sum}$	$\displaystyle \int 3x^{-3}dx + \int 4x^{5}dx$
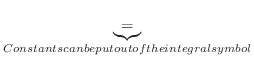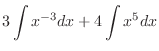	$\displaystyle \underbrace{=}_{Constants can be put out of the integral symbol}$	$\displaystyle 3\int x^{-3}dx + 4\int x^{5}dx$
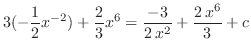	$\displaystyle =$	$\displaystyle 3(-\frac{1}{2}x^{-2}) + \frac{2}{3}x^6 = \frac{-3}{2\,{x^2}} + \frac{2\,{x^6}}{3} + c$

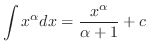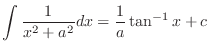(b) Note that the integration formulae $\displaystyle{\int x^{\alpha}dx = \frac{x^{\alpha}}{\alpha + 1} + c}$ and $\displaystyle{\int \frac{1}{x^{2} + a^{2}}dx = \frac{1}{a}\tan^{-1}{x} + c}$ .

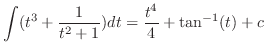
$\displaystyle \int (t^3 + \frac{1}{t^2 + 1}) dt = \frac{t^4}{4} + \tan^{-1} (t) + c$

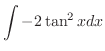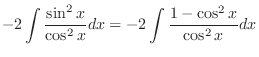$\displaystyle \int -2 \tan^{2}{x} dx$	$\displaystyle =$	$\displaystyle -2 \int \frac{\sin^{2}{x}}{\cos^{2}{x}} dx = -2 \int \frac{1 - \cos^{2}{x}}{\cos^{2}{x}}dx$
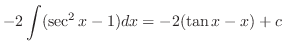	$\displaystyle =$	$\displaystyle -2 \int (\sec^{2}{x} - 1)dx = -2(\tan{x} - x) + c$

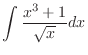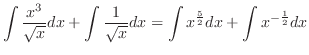$\displaystyle \int \frac{x^3 + 1}{\sqrt{x}} dx$	$\displaystyle =$	$\displaystyle \int \frac{x^{3}}{\sqrt{x}}dx + \int \frac{1}{\sqrt{x}}dx = \int x^{\frac{5}{2}}dx + \int x^{-\frac{1}{2}} dx$
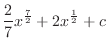	$\displaystyle =$	$\displaystyle \frac{2}{7}x^{\frac{7}{2}} + 2x^{\frac{1}{2}} + c$

(e) If the order of the numerator is greater than or equal to the denominator, divide it.．

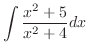$\displaystyle \int \frac{x^2 + 5}{x^2 + 4} dx$

$\displaystyle =$

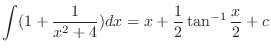$\displaystyle \int (1 + \frac{1}{x^2 + 4}) dx = x + \frac{1}{2}\tan^{-1}{\frac{x}{2}} + c$

(f) Note that $\displaystyle{\int \frac{1}{\sqrt{a^{2} - x^{2}}}dx = \sin^{-1}{\frac{x}{a}} + c}$ ．

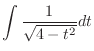$\displaystyle \int \frac{1}{\sqrt{4 - t^2}} dt$

$\displaystyle =$

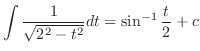$\displaystyle \int \frac{1}{\sqrt{2^2 - t^2}} dt = \sin^{-1}{\frac{t}{2}} + c$

(g) Write $\displaystyle{\cos^{2}{x} = \frac{1 + \cos{2x}}{2}}$ . Then we can use $\displaystyle{\int \cos{bx} dx = \frac{1}{b}\sin{x} + c}$ ．

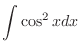$\displaystyle \int \cos^{2}{x} dx$

$\displaystyle =$

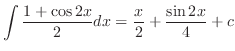$\displaystyle \int \frac{1 + \cos{2x}}{2} dx = \frac{x}{2} + \frac{\sin{2x}}{4} + c$

(h) Note that $\displaystyle{\int \frac{1}{\sqrt{x^{2} + A}}dx = \log{\vert x + \sqrt{x^{2} + A}\vert} + c}$ ．

$\displaystyle \int \frac{1}{\sqrt{t^2 + 4}} dt = \log{\vert t + \sqrt{t^2 + 4}\vert} + c$

(i) Note that $\displaystyle{\int \frac{1}{x^{2} - a^{2}}dx = \frac{1}{2a}\log{\vert\frac{x-a}{x+a}}\vert + c}$ .

$\displaystyle \int \frac{1}{4 - x^2} dx = - \int \frac{1}{x^{2} - 2^{2}}dx = -\frac{1}{4}\log{\left\vert\frac{x-2}{x+2}\right\vert} + c$