Next: Curve sketching) Up: 微分法(DEFFERENTIATION) Previous: Properties of functions
2.5
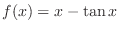 より,
より,
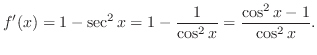
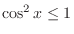 and the equality holds at
and the equality holds at 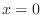 .Thus,
.Thus,
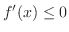 . Thus,
. Thus, 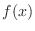 is strictly monotonically decreasing on
is strictly monotonically decreasing on
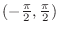 .
.
2.
(a) Let
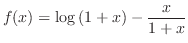 . Then
. Then 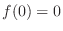 . Now for
. Now for 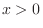 , we show
, we show 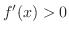 .
.
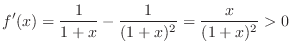
(b) Let
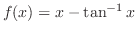 . Then
. Then 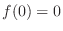 . Now for
. Now for 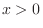 , we show
, we show 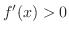 .
.
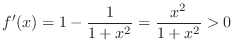
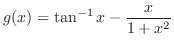 . Then
. Then 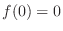 . Now for
. Now for 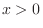 , we show
, we show 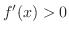 .
.
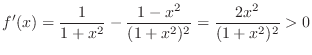
(c) Take logarithm on both sides,we show
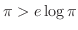 . Let
. Let
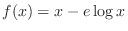 . Then
. Then 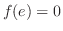 .Also, for
.Also, for 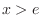 , we have
, we have
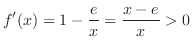
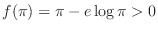
3.
(a) Local maximum 7 at 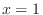 ,local minimum 3 at
,local minimum 3 at 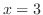 .
.
(b) Local minimum 0 at 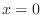 , local maximum
, local maximum
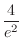 at
at 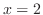 .
.
![\begin{figure}\begin{center}
\includegraphics[width=8cm]{CALCFIG/Fig9-2-6-3.eps}
\end{center}\end{figure}](img554.png)