Next: Mean-value theorem Up: 微分法(DEFFERENTIATION) Previous: Higher-order derivatives
2.3
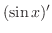 |
 |
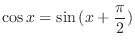 |
|
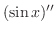 |
 |
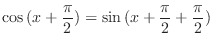 |
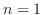 , this is ture.
Now assume that
, this is ture.
Now assume that
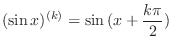
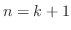 .
.
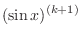 |
 |
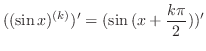 |
|
 |
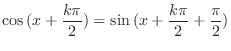 |
||
 |
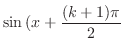 |
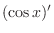 |
 |
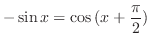 |
|
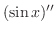 |
 |
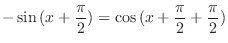 |
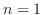 , this is true. Now assume that
, this is true. Now assume that
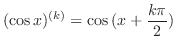
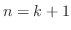 .
.
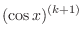 |
 |
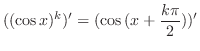 |
|
 |
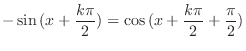 |
||
 |
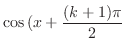 |
1.(c)
Using the mathematical induction, we prove this. For 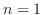 ,
,
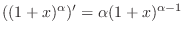
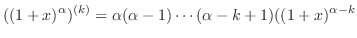
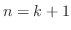 .
.
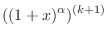 |
 |
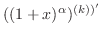 |
|
 |
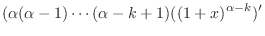 |
||
 |
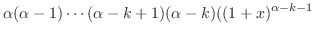 |
||
 |
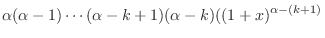 |
2.
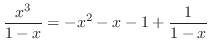 また
また
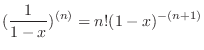 より
より
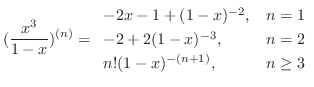
(b) By Leibniz's theorem, we have
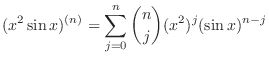
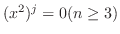 . Then
. Then
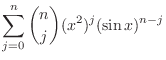 |
 |
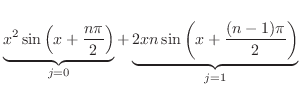 |
|
 |
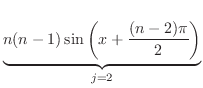 |
(c) By Leibniz's theorem, we have
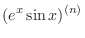 |
 |
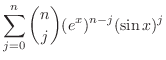 |
|
 |
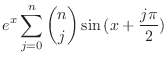 |
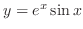 , we can write
, we can write
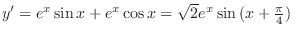 .So, we suppose that
.So, we suppose that
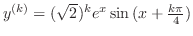 . Then
. Then
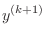 |
 |
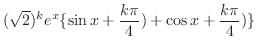 |
|
 |
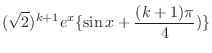 |