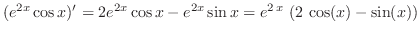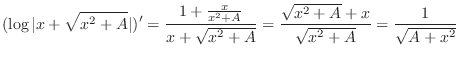Next: Higher-order derivatives Up: 微分法(DEFFERENTIATION) Previous: 2.2.1 Answer
2.2.2
1.
(a)
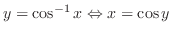 . Then
. Then
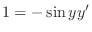 . Now solve for
. Now solve for 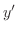 . Then
. Then
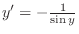 .Pay attention to the range of
.Pay attention to the range of 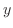 , express
, express 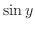 using
using  . Then we have
. Then we have
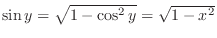 .Therefore,
.Therefore,
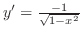
(b)
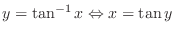 implies that
implies that
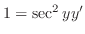 . Now solve this for
. Now solve this for 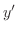 . Then
. Then
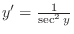 .Pay attention to the range of
.Pay attention to the range of 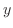 , express
, express
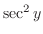 using
using  . Then
. Then
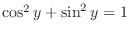 . Thus,
. Thus,
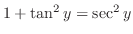 .Therefore,
.Therefore,
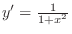
2.
(a)
Take logarithm on both sides. Then
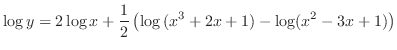
Differentiate both sides with respect to  .
.
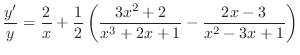
Thus,
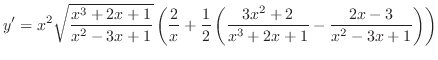
(b)Take logarithm on both sides. Then
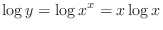
Now differentiate both sides with respect to  .
.
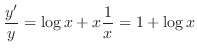
Thus,
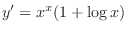
(c)Take logarithm on both sides. Then
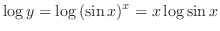
Now differentiate both sides with respect to  .
.
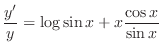
Thus,
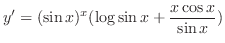
(d)Take logarithm on both sides. Then
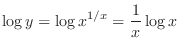
Now differentiate both sides with respect to  .
.
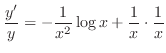
Thus,
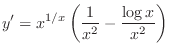
3.
4.
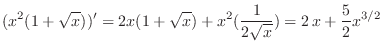
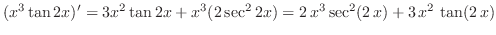
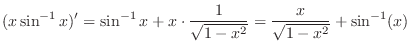
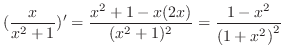
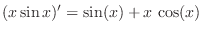
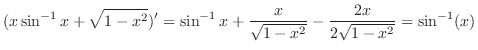
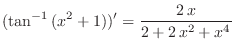
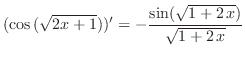
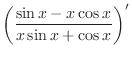 |
 |
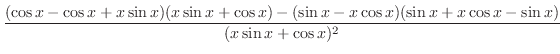 |
|
 |
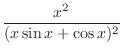 |