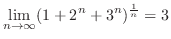Next: Euler e Up: FUNCTIONS Previous: Sequences
1.6
1.
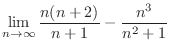 |
 |
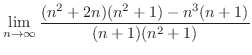 |
|
 |
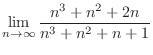 |
||
 |
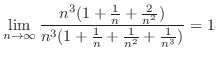 |
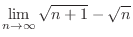 |
 |
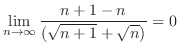 |
Note that for 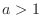 , we have
, we have
![$\sqrt[n]{a} > 1$](img270.png) . Thus, we can set
. Thus, we can set
![$\sqrt[n]{a} = 1 + h, \ h > 0$](img271.png) . Then
. Then
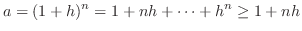
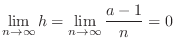
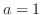 ÅCwe have
ÅCwe have
![$\sqrt[n]{a} = 1$](img275.png) for all
for all 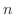 . Thus,
. Thus,
![$\displaystyle \lim_{n \rightarrow \infty}\sqrt[n]{a} = 1 $](img277.png)
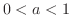 , we let
, we let
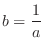 . Then
. Then 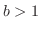 and
and
![$\displaystyle 1 = \lim_{n \rightarrow \infty}\sqrt[n]{b} = \lim_{n \rightarrow \infty}\frac{1}{\sqrt[n]{a}} $](img281.png)
3.
(a)
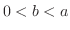 implies
implies
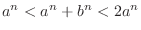 ÅD Then,
ÅD Then,
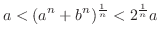 ÅD Thus,
ÅD Thus,
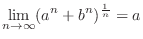 .
.
(b)
Since
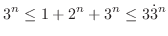 , we take
, we take 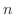 th root. Then
th root. Then
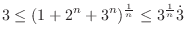 ÅDAs
ÅDAs
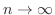 ,
,
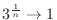 . Then by squeezing theorem, we have
. Then by squeezing theorem, we have