1.4 Answer

1.4

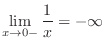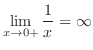(a) $\displaystyle{\lim_{x \to 0-} \frac{1}{x} = - \infty}$ and $\displaystyle{\lim_{x \to 0+} \frac{1}{x} = \infty}$ ． Thus, the limit does not exist.

(b) $\displaystyle{\lim_{x \to 0} \frac{1}{x^2} = \infty}$

(c)

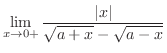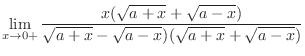$\displaystyle \lim_{x \to 0+} \frac{\vert x\vert}{\sqrt{a+x} - \sqrt{a - x}}$	$\displaystyle =$	$\displaystyle \lim_{x \to 0+} \frac{x(\sqrt{a +x} + \sqrt{a-x})}{\sqrt{a+x} - \sqrt{a - x})(\sqrt{a+x} + \sqrt{a-x})}$
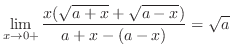	$\displaystyle =$	$\displaystyle \lim_{x \to 0+}\frac{x(\sqrt{a+x} + \sqrt{a-x})}{a+x - (a-x)} = \sqrt{a}$

(d)

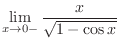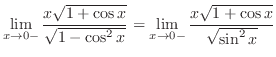$\displaystyle \lim_{x \to 0-}\frac{x}{\sqrt{1 - \cos{x}}}$	$\displaystyle =$	$\displaystyle \lim_{x \to 0-} \frac{x\sqrt{1 + \cos{x}}}{\sqrt{1 - \cos^{2}{x}}} = \lim_{x \to 0-}\frac{x \sqrt{1 + \cos{x}}}{\sqrt{\sin^{2}{x}}}$
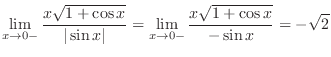	$\displaystyle =$	$\displaystyle \lim_{x \to 0-}\frac{x \sqrt{1 + \cos{x}}}{\vert\sin{x}\vert} = \lim_{x \to 0-}\frac{x \sqrt{1 + \cos{x}}}{-\sin{x}} = - \sqrt{2}$

(e) $\displaystyle{\lim_{x \to \infty} \frac{1}{x} = 0}$ ，Since $\cos{x}$ is continuous， $\displaystyle{\lim_{x \to \infty} \cos{\frac{1}{x}} = \cos(\lim_{x \to \infty} \frac{1}{x}) = 1}$

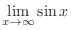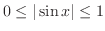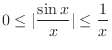(f) $\displaystyle{\lim_{x \to \infty} \sin{x}}$ vibrates. Since $0 \leq \vert\sin{x}\vert \leq 1$ . Thus， $\displaystyle{0 \leq \vert\frac{\sin{x}}{x}\vert \leq \frac{1}{x}}$ .

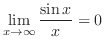
Therefore, $\displaystyle{\lim_{x \to \infty} \frac{\sin{x}}{x} = 0}$

(g) 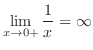$\displaystyle{\lim_{x \to 0+} \frac{1}{x} = \infty}$ suggest that 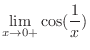$\displaystyle{\lim_{x \to 0+} \cos(\frac{1}{x})}$ does not exist. To show this, let 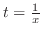$t = \frac{1}{x}$ . Then 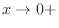$x \to 0+$ implies 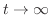$t \to \infty$ . Then 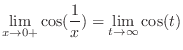$\displaystyle{\lim_{x \to 0+} \cos(\frac{1}{x}) = \lim_{t \to \infty} \cos(t)}$ and the limit does not exist.