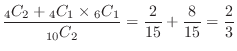Next: Probability axiom Up: Probabilistic model Previous: Probabilistic model Contents
 . Of the events, those that cannot be decomposed into simpler ones are called elementary events..
. Of the events, those that cannot be decomposed into simpler ones are called elementary events..
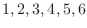
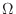 is
is
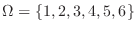 .Here, considering the event
.Here, considering the event 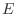 that the number of pits is even.,
that the number of pits is even.,
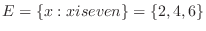
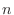 of elementary events in the sample space
of elementary events in the sample space 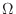 that can occur in a trial, and it is equally likely that any of them will occur. At this time. When the number of elementary events in which an event
that can occur in a trial, and it is equally likely that any of them will occur. At this time. When the number of elementary events in which an event 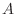 occurs is
occurs is 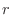 , the probability that the event
, the probability that the event 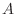 will occur is defined by
will occur is defined by
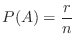
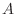 occurs
occurs 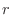 times when a trial is repeated
times when a trial is repeated 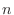 times. Now, when increasing the number of trials
times. Now, when increasing the number of trials 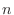 , if the relative frequency
, if the relative frequency 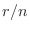 approaches a certain value
approaches a certain value 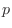 , the probability that the event
, the probability that the event 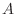 will occur is defined as
will occur is defined as 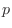 . This is called statistical probability.
. This is called statistical probability.
(a) Find the probability using the number of cases. 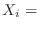 [1 pit i times out of 6 times].
[1 pit i times out of 6 times].
If you throw the dice 6 times, there are a total of
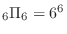 . Next, let's count how many times there are cases where the 1st roll appears once out of 6 times.
. Next, let's count how many times there are cases where the 1st roll appears once out of 6 times.
If you get a 1 on the first throw, the remaining 5 times are other than 1. Then
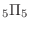 .Similarly for 2nd, 3rd,4th, Thus,
.Similarly for 2nd, 3rd,4th, Thus,
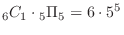
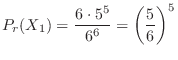
(b) There are a total of
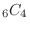 combinations in which 1's are rolled 4 times. At that time, the remaining two times are other than 1, so
combinations in which 1's are rolled 4 times. At that time, the remaining two times are other than 1, so 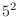 . So in total
. So in total
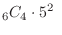 ways
ways
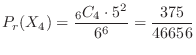
(d) The number of 1's that appear 5 times or more is
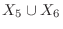
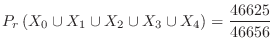
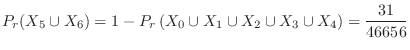
2.
(a) There is no choice but to take out 4 out of the 5 white balls in the bag,The combination is
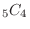 .
Therefore, the probability that all four taken out are white balls is
.
Therefore, the probability that all four taken out are white balls is
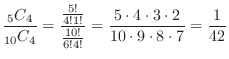
(b) Two balls are white when 2 white balls are selected from 5 white balls and two balls are from red and black balls. Thus the number of outcomes is
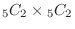 .Therefore, the probability that white is exactly 2 out of the 4 taken out is
.Therefore, the probability that white is exactly 2 out of the 4 taken out is
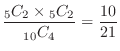
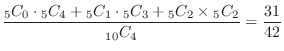
(d) The combination of two whites and two reds is
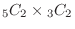 . Therefore, the probability that white is 2 and red is 2 out of the 4 taken out is
. Therefore, the probability that white is 2 and red is 2 out of the 4 taken out is
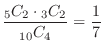
(e) Pay attention to the 4 balls taken out.
1. The fact that white, red, and black are all included means that one of white, red, and black can be considered as a combination of two. Thus
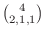 .
.
2. The probability of taking out one white, one red, one black is
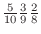 .
.
3.Therefore, the probability that white, red, and black are included is
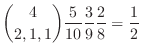
3.
(a) Let's think about how many ways to arrange 1 to 10 in a row.
There can be any of 1 to 10 at the beginning, so there are 10 ways,Next is 9 ways  ,The total is
,The total is
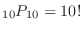 ways.
ways.
Thus the probability of 1 to 10 are lined up in that order is
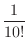
(b) The fact that the 4 card is exactly the 4th means that the other 9 cards can be anywhere, so the 4th card is exactly the 4th card in
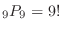 Street There is. Therefore, the probability is
Street There is. Therefore, the probability is
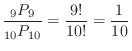
(c) The fact that 1 is first and 4 is fourth means that the other eight cards can be anywhere, so there are a total of
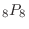 ways. Therefore, the probability that 1 will come first and 4 will come fourth is
ways. Therefore, the probability that 1 will come first and 4 will come fourth is
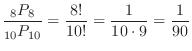
4. (a) The radius of the disk is more than 1.5 cm. To fit inside a square, the center of the disk should be inside a square with a side of 5 cm. Therefore, the probability is
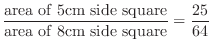
(b) The complement of A = 「The disk touches the side of the square」is 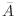 = 「The disk is inside the square.Thus the probability is,
= 「The disk is inside the square.Thus the probability is,
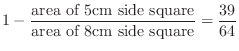
(c) In order for a disk to span four squares, its center must be within 1.5 cm of the boundary of the four squares. The area is
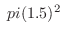 . Therefore, the probability that a disk will span four squares is
. Therefore, the probability that a disk will span four squares is
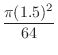
5.
(a) There are only two out of the four white balls in the bag, so the combination is
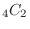 . Therefore, the probability that the two taken out are both white balls is
. Therefore, the probability that the two taken out are both white balls is
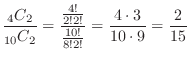
(b) Only one white ball is the number when one is taken out from four white balls and one is taken out from six red balls.Then
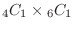 .Thus,
.Thus,
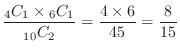
(c) The event that at least one is a white ball is either both white balls or only one white ball. Note that these events are mutual exclusivity events (which do not occur at the same time), in total.,
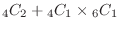 ways.Thus the probability is
ways.Thus the probability is