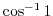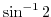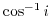Inverse function of elementary function

Exercise2.4

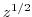1. Show that $z^{1/2}$ has two branches.

2. Find all of the following values.

(a)

$\log{2}$

(b)

$\log{(-1)}$

(c)

$\log{i}$

(d)

$\log(1+i)$

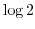
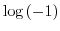
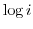
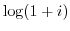
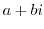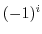
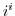
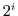
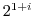
3. Express the following value in the form of $a + bi$.

(a)

$(-1)^{i}$

(b)

$i^{i}$

(c)

$2^{i}$

(d)

$2^{1+i}$

4. Prove the following formulas.

(a)

$\sin^{-1}{z} = \frac{1}{i}\log{(iz \pm \sqrt{1 - z^2})}$

(b)

$\tan^{-1}{z} = \frac{1}{2i}\log{\frac{1 + iz}{1 - iz}}$

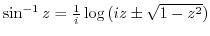
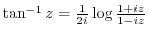
(5) Find the following values.

(a)

$\cos^{-1}{1}$

(b)

$\sin^{-1}{2}$

(c)

$\cos^{-1}{i}$