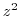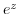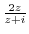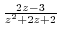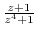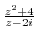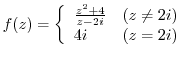Limit and Continuity

Exercise3.1

1. Find out if the next set of points is a region

(a)

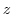$z$ set of points on plane excluding 0

(b)

$\{z : \Re{z} > 0\}$

(c)

$\{z : \Im {z} \geq 0\}$

(d)

$\{z : 1 < \vert z\vert < 2\}$

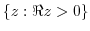
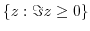
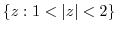
2. Find the limit of the followings.

(a)

$${\lim_{z \to i}(z^2 + 2z)}$$

(b)

$${\lim_{z \to \frac{i}{2}}\frac{(2z-3)(z+i)}{(iz - 1)^2}}$$

(c)

$${\lim_{z \to 1+i}\frac{z - 1 -i}{z^2 - 2z + 2}}$$

(d)

$${\lim_{z \to e^{i\pi/4}}\frac{z^2}{z^4 + z + 1}}$$

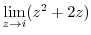
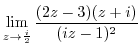
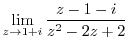
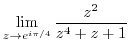
3. Find the point where the following function is not continuous.

(a)

$z^2$

(b)

$e^z$

(c)

$\frac{2z}{z+ i}$

(d)

$\frac{2z - 3}{z^2 + 2z + 2}$

(e)

$\frac{z+1}{z^4 + 1}$

(f)

$\frac{z^2 + 4}{z - 2i}$

(g)

$f(z) = \left\{\begin{array}{ll} \frac{z^2 + 4}{z - 2i} & (z \neq 2i)\\ 4i & (z = 2i) \end{array}\right.$