Next: 3.2 Analytic function Up: Solution Previous: 2.4 Inverse function of Index
1.
In order for the set  to be called a region, it must satisfy the following two conditions.
to be called a region, it must satisfy the following two conditions.
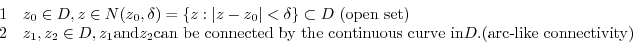
Note
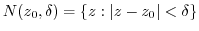 is said to be a
is said to be a 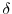 neighborhood of a point
neighborhood of a point 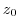 .
.
(a) Let  be the set of the
be the set of the 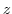 plane minus the origin O.
plane minus the origin O.
1. If you select a point 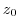 other than the origin and let
other than the origin and let 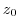 and half the distance to the origin
and half the distance to the origin 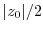 be
be 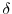 , then the
, then the 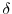 neighborhood
neighborhood
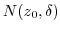 is in
is in  . Thus
. Thus  is open set.
is open set.
2. Any two points in  can be connected by the continuous curve contained in
can be connected by the continuous curve contained in  , so arc-like connectivity is satisfied.
, so arc-like connectivity is satisfied.
Therefore,  is a region.
is a region.
1. Choose 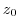 other than the origin. Let
other than the origin. Let 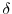 be the half of the distance from
be the half of the distance from 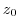 to the imaginary axis. The
to the imaginary axis. The 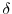 neighborhood
neighborhood
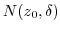 is in
is in  . Thus,
. Thus,  is an open set.
is an open set.
2. Any two points in  can be connected by the continuous curve contained in
can be connected by the continuous curve contained in  , so arc-like connectivity is satisfied.
, so arc-like connectivity is satisfied.
Thus,  is a region.
is a region.
1. If we choose 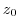 on the real axiz, then for any
on the real axiz, then for any 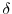 neighborhoos
neighborhoos
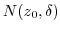 contains a point other that
contains a point other that  . Thus it is not a open set. But, any point in
. Thus it is not a open set. But, any point in
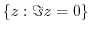 ,
, 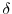 neighborhood of its point contains a point in
neighborhood of its point contains a point in  and not in
and not in  . A collection of such points is calledboundary of
. A collection of such points is calledboundary of  . Thus,
. Thus,  is a closed set.
is a closed set.
2. Any two points in  can be connected by the continuous curve contained in
can be connected by the continuous curve contained in  , so arc-like connectivity is satisfied.
.
, so arc-like connectivity is satisfied.
.
Therefore,  is a closed set.
is a closed set.
1. Choose 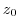 other than the origin. Then let
other than the origin. Then let 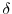 be half of the distance of the shorter of two: the distance from
be half of the distance of the shorter of two: the distance from 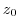 to
to 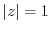 or to
or to 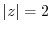 . Then
. Then 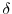 neighborhood
neighborhood
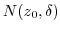 is in
is in  . Therefore,
. Therefore,  is an open set.
is an open set.
2. Any two points in  can be connected by the continuous curve contained in
can be connected by the continuous curve contained in  , so arc-like connectivity is satisfied. .
, so arc-like connectivity is satisfied. .
Therefore,  is a region.
is a region.
2.
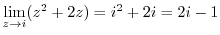
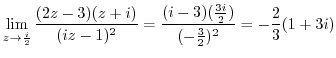
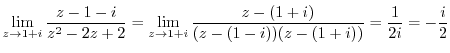
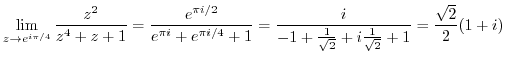
3.
Note
1. The exponential function 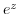 is continuous at all points on the complex plane, the logarithmic function
is continuous at all points on the complex plane, the logarithmic function 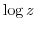 is continuous except at the origin, and the meromorphic function is continuous except when the denominator is 0
is continuous except at the origin, and the meromorphic function is continuous except when the denominator is 0
2. The sum, difference, product, and composition of continuous functions are also continuous, the denominator is non-zero, and the quotient is also continuous.
(a) 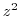 is a meromorphic function. Thus, it is continuous on all points.
is a meromorphic function. Thus, it is continuous on all points.
(b) 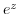 is continuous at all points..
is continuous at all points..
(c)
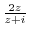 is a meromorphic function. Thus it is discontinuous at
is a meromorphic function. Thus it is discontinuous at 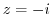 .
.
(d)
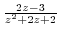 is a meromorphic function. Thus it is discontinuous ar
is a meromorphic function. Thus it is discontinuous ar
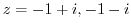 .
.
(e)
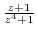 is a meromorphic function. Thus it is discontinuous at the point where
is a meromorphic function. Thus it is discontinuous at the point where
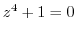 .
.
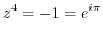 implies
implies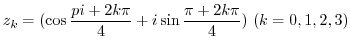
Therefore,
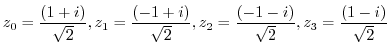
(f)
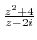 is a meromorphic function. Thus it is discontinuous at
is a meromorphic function. Thus it is discontinuous at 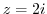 .
.
(g)
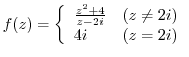 is meromorphic function except at
is meromorphic function except at 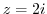 . Thus it is continuous except at
. Thus it is continuous except at 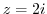 . Note that
. Note that 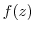 is a piecewise function. Thus to check to see if it is continuous, we have to go back to the definition. In other words, if
is a piecewise function. Thus to check to see if it is continuous, we have to go back to the definition. In other words, if
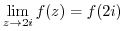
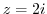 .
.
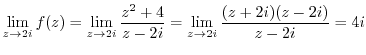
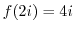 . Thus it is continuous at
. Thus it is continuous at 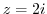 .
.