Next: 演習問題8.2 Up: フーリエ変換(Fourier transformations) Previous: 演習問題8.1 目次 索引
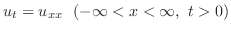
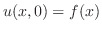
解
この方程式は変数分離法でも解けるが,ここではフーリエ変換を用いて解く.まず
![${\cal F}[u(x,t)] = U(\omega,t)$](img2461.png) と表わす.次に偏微分方程式の両辺にフーリエ変換を施すと,左辺は
と表わす.次に偏微分方程式の両辺にフーリエ変換を施すと,左辺は
![$\displaystyle {\cal F}[u_{t}] = \int_{-\infty}^{\infty}u_{t}e^{-i \omega x}dx =...
...^{\infty}u(x,t)e^{-i \omega x}dx = \frac{\partial}{\partial t}[U(\omega ,t)] . $](img2462.png)
![$\displaystyle {\cal F}[u_{xx}] = (i \omega)^{2}U(\omega, t) . $](img2463.png)
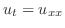 は次の常微分方程式に変換される.
は次の常微分方程式に変換される.
![$\displaystyle \frac{d}{dt}[U(\omega ,t)] + \omega^{2}U(\omega, t) = 0 $](img2465.png)
 について線形なので,一般解
について線形なので,一般解
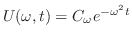
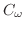 を求めると,
を求めると,
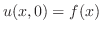 より
より
![$\displaystyle {\cal F}[u(x,0)] = U(\omega,0) = F(\omega) = C_{\omega} . $](img2468.png)
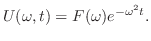
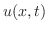 を求めると
を求めると
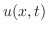 |
 |
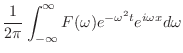 |
|
 |
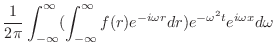 |
||
 |
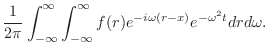 |
![$\displaystyle e^{-i \omega(r-x)} = \cos{[\omega(r-x)]} - i \sin{[\omega(r-x)]} $](img2473.png)
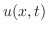 |
 |
![$\displaystyle \frac{1}{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(r)\cos{[\omega(r-x)]}e^{- \omega^{2} t}dr d\omega$](img2474.png) |
|
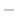 |
![$\displaystyle \frac{i}{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(r)\sin{[\omega(r-x)]}e^{- \omega^{2} t}dr d\omega .$](img2475.png) |
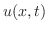 は実数であることに注意すると,虚部が消えて
は実数であることに注意すると,虚部が消えて
![$\displaystyle u(x,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f(r)\cos{[\omega(r-x)]}e^{- \omega^{2} t}dr d\omega $](img2476.png)

 で与えられている.弦の初速度が0のとき,この弦の垂直方向の変位を求めよ.
で与えられている.弦の初速度が0のとき,この弦の垂直方向の変位を求めよ.
解
この弦の垂直方向の変位を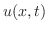 とすると,
とすると,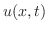 は
一次元波動方程式
は
一次元波動方程式
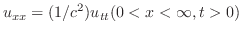
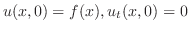
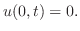
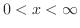 より,フーリエ正弦変換を用いる.演習問題8.1.1より
より,フーリエ正弦変換を用いる.演習問題8.1.1より
![$\displaystyle {\cal F}_{s}[u_{xx}]$](img2480.png) |
 |
![$\displaystyle - \omega {\cal F}_{c}[u_{x}]$](img2481.png) |
|
 |
![$\displaystyle - \omega (- u(0+,t) + \omega {\cal F}_{s}[u])$](img2482.png) |
||
 |
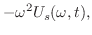 |
||
![$\displaystyle \frac{1}{c^2}{\cal F}_{s}[u_{tt}]$](img2484.png) |
 |
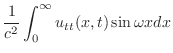 |
|
 |
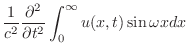 |
||
 |
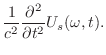 |
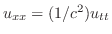 は次の常微分方程式に変換される.
は次の常微分方程式に変換される.
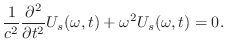
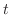 について線形なので,一般解
について線形なので,一般解
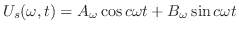
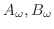 を求めると,
を求めると,
 より
より
![$\displaystyle {\cal F}_{s}[u(x,0)] = U_{s}(\omega.0) = A_{\omega} = F_{s}(\omega) . $](img2492.png)
![$\displaystyle {\cal F}_{s}[u_{t}(x,0)] = \frac{\partial U_{s}(\omega.0)}{\partial t} = c\omega B_{\omega} = 0 $](img2493.png)
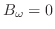 .よって
.よって
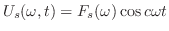 を得る.ここでフーリエ反転公式を用いると
を得る.ここでフーリエ反転公式を用いると
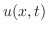 |
 |
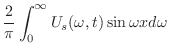 |
|
 |
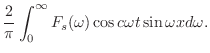 |
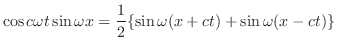
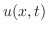 |
 |
![$\displaystyle \frac{1}{\pi}\int_{0}^{\infty}F_{s}(\omega)[\sin{\omega(x+ct)} + \sin{\omega(x-ct)}] d\omega$](img2499.png) |
|
 |
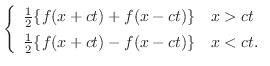 |