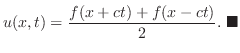Next: 演習問題7.2 Up: 偏微分方程式(partial differential equations) Previous: 演習問題7.1 目次 索引
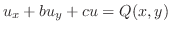
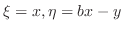 を用いることにより
を用いることにより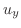 の項を落とすことができるので,その解は常微分方程式
の項を落とすことができるので,その解は常微分方程式
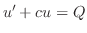
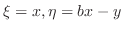
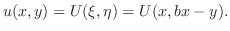
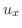 |
 |
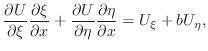 |
|
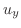 |
 |
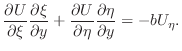 |
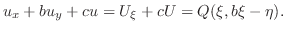
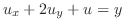 を解け.
を解け.
解
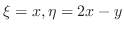 とおくと
とおくと
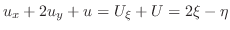
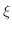 について1階線形なので積分因子
について1階線形なので積分因子
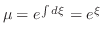 より,
より,
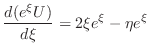
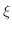 で積分すると,
で積分すると,
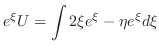 |
 |
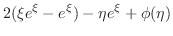 |
|
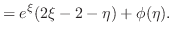 |
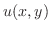 |
 |
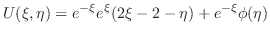 |
|
 |
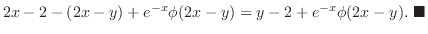 |
次の解法は変数分離法(method of separation of variables)とよばれるもので,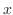 の関数
の関数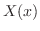 と
と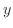 の関数
の関数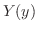 の積の形の解
の積の形の解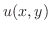 を捜す方法です.
を捜す方法です.
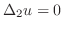 を解け.
を解け.
解
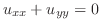 を
を
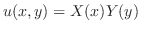 を用いて解く.
を用いて解く.
まず
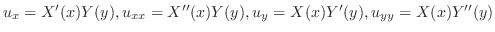 より
より
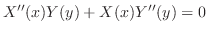
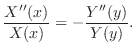
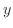 と独立で右辺は
と独立で右辺は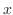 と独立.それが等しいということはともに同じ定数ということがいえる.この定数を
と独立.それが等しいということはともに同じ定数ということがいえる.この定数を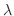 とおくと
とおくと
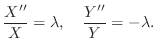
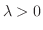 のとき
のとき
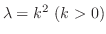 とおくと
とおくと
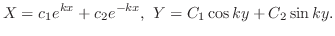
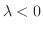 のとき
のとき
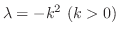 とおくと
とおくと
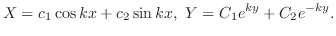
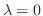 のとき
のとき
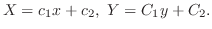
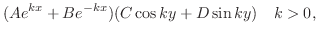
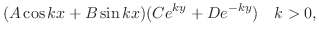
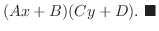
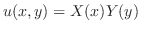 を代入することにより
を代入することにより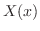 と
と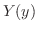 を分離できる微分方程式を変数分離形(separation of variables)といいます.
を分離できる微分方程式を変数分離形(separation of variables)といいます.
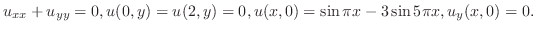
解
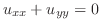 よりさきほどの例題の結果が使えます.初期条件
よりさきほどの例題の結果が使えます.初期条件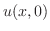 の形より3つの解の中から
の形より3つの解の中から
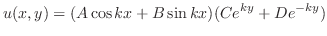
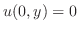 より
より
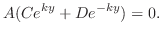
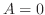 または
または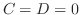 .しかし
.しかし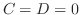 なら
なら
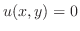 となるので
となるので
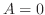 とおくと
とおくと
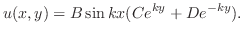
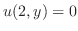 を用いると
を用いると
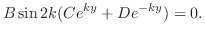
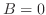 または
または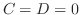 なら
なら
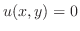 となるので
となるので
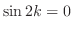 よって
よって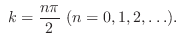
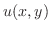 |
 |
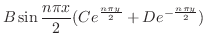 |
|
 |
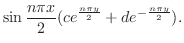 |
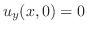 を用いるために両辺を
を用いるために両辺を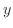 で偏微分すると
で偏微分すると
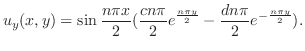
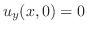 より
より
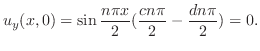
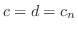 .これよりここまでの条件を満たす解の列
.これよりここまでの条件を満たす解の列
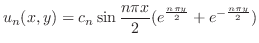
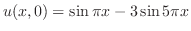 を満たすために,
を満たすために,
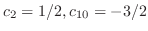 その他の
その他の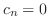 とおき,重ね合わせの原理を用いると
とおき,重ね合わせの原理を用いると
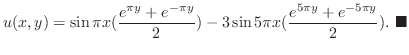
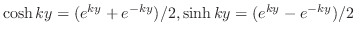 を用いると
を用いると
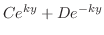 の代わりに
の代わりに
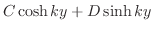 が使えます.
が使えます.
次の例題が示すように,変数分離法は変数係数の偏微分方程式にも使えます.
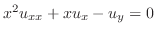 を解け.
を解け.
解
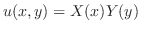 を与えられた方程式に代入すると
を与えられた方程式に代入すると
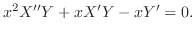
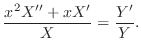
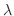 とおくと
とおくと
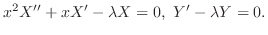
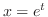 とおくことにより解が得られる.
とおくことにより解が得られる.
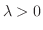 のとき
のとき
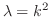 とおくと
とおくと
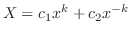 ,
,
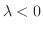 のとき
のとき
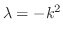 とおくと
とおくと
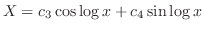 ,
,
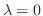 のときは
のときは
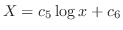 となる.
となる.
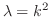 とおくと
とおくと
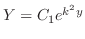 ,
,
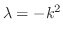 とおくと
とおくと
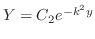 ,
,
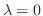 のときは
のときは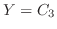 となる.
したがって,
となる.
したがって,
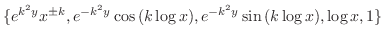

偏微分方程式のすべてが変数分離形になるわけではありません.たとえば
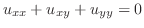
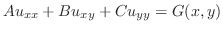
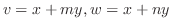 とおくことにより,
とおくことにより,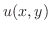 を
を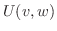 と
と
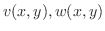 の合成関数とし,
の合成関数とし,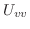 と
と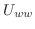 の係数が0になるように
の係数が0になるように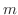 と
と
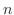 を選ぶことにより
を選ぶことにより
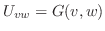 を求めるという方法です.次の例題で詳しく示してみましょう.
を求めるという方法です.次の例題で詳しく示してみましょう.
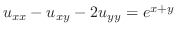 を解け.
を解け.
解
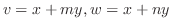 とおくと
とおくと
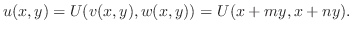
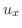 |
 |
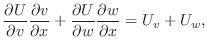 |
|
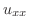 |
 |
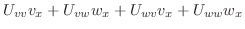 |
|
 |
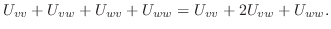 |
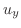 |
 |
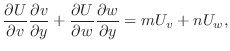 |
|
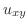 |
 |
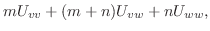 |
|
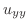 |
 |
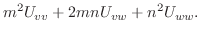 |
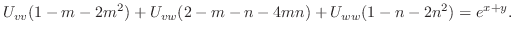
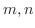 を二次方程式
を二次方程式
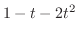 の異なる実数解とすると
の異なる実数解とすると
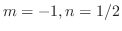 .
これより
.
これより
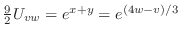 を得る.これを解くと
を得る.これを解くと
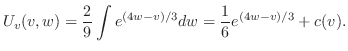
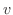 で積分すると
で積分すると
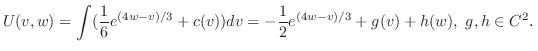
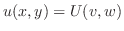 |
 |
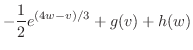 |
|
 |
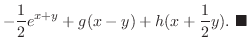 |
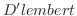 法を用いて波動方程式
法を用いて波動方程式
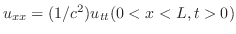 の解で初期条件
の解で初期条件
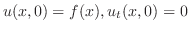
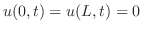
解
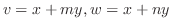 とおくと
とおくと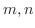 は二次方程式
は二次方程式
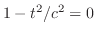 の解になるので
の解になるので
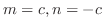 .よって
.よって
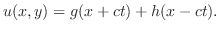
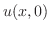 |
 |
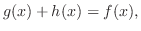 |
|
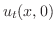 |
 |
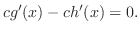 |
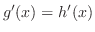 .よって
.よって
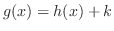 ,ただし
,ただし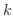 はある定数.この
はある定数.この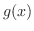 を上の2つの式の最初のほうに代入すると
を上の2つの式の最初のほうに代入すると
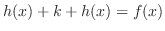
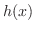 |
 |
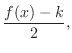 |
|
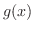 |
 |
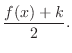 |