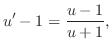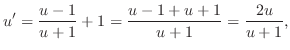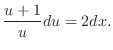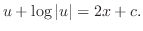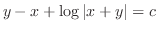Next: 演習問題1.3 Up: 1階微分方程式(1st order linear differential Previous: 演習問題1.2 目次 索引
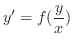
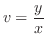
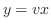 より
より
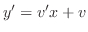 となり,これを元の微分方程式に代入すると
となり,これを元の微分方程式に代入すると
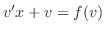
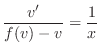
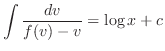
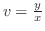 を代入すると一般解を得ます.
を代入すると一般解を得ます.
与えられた微分方程式が同次形か見分けるには次のようにすると簡単です.
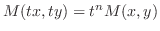 を満たす関数
を満たす関数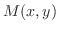 を
を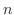 次の同次関数(homogeneous function)といいます.この定義を用いると微分方程式
次の同次関数(homogeneous function)といいます.この定義を用いると微分方程式
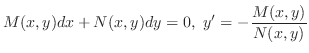
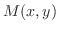 と
と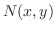 が同じ次数の同次関数ならば,与えられた微分方程式は同次形です.
が同じ次数の同次関数ならば,与えられた微分方程式は同次形です.
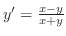 を解け.
を解け.
解
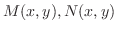 ともに一次の同次関数. 右辺の分子と分母を
ともに一次の同次関数. 右辺の分子と分母を で割ると
で割ると
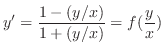
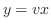 とおくと,
とおくと,
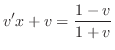
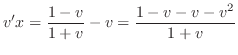
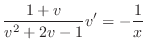
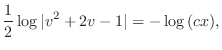
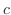 は任意定数.よって
は任意定数.よって
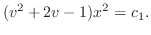
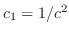 より任意定数.最後に
より任意定数.最後に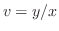 に置き換えて整理すると,一般解は
に置き換えて整理すると,一般解は
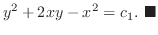
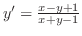 を解け.
を解け.
解 これは同次形ではないが,定数項が落ちれば同次形である.そこで次のようにして同次形に変形できる.2直線
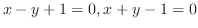
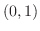 である.この点を原点とするように座標軸の平行移動
である.この点を原点とするように座標軸の平行移動
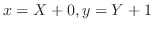
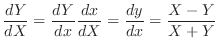
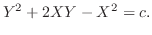
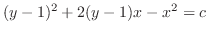

変換によって微分方程式を同次形に直すとき,与えられた微分方程式の形から何をどうおくか明らかなものもあります.
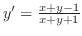 を解け.
を解け.
解
分母と分子に表われている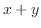 より,
より,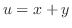 と置く.すると
と置く.すると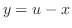 より
より
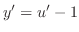 . これを元の微分方程式に代入すると,
. これを元の微分方程式に代入すると,