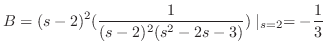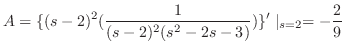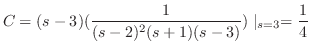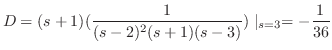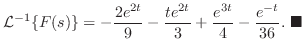Next: 演習問題5.4 Up: ラプラス変換(The Laplace transformation) Previous: 演習問題5.3.2 目次 索引
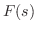 が与えられたとき,ラプラス変換が
が与えられたとき,ラプラス変換が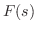 となるような関数
となるような関数 を求める準備ができました.
を求める準備ができました.
|
定義 5..4
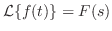 となるような となるような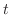 の関数 の関数 が存在するとき, が存在するとき, を を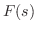 のラプラス逆変換といい,次のようにあらわします. のラプラス逆変換といい,次のようにあらわします.
![$\displaystyle {\cal L}^{-1}[F(s)] = f(t) . $](img1552.png)
|
ラプラス逆変換を求めるとき,次の変換表は便利です.
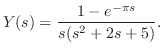
解
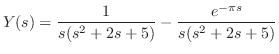
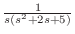 の逆変換を求める.
の逆変換を求める.
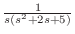 を部分分数分解すると
を部分分数分解すると
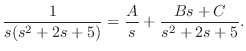
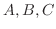 の求め方はいろいろありますが,ここでは次のようにして求めます.
の求め方はいろいろありますが,ここでは次のようにして求めます.
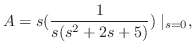
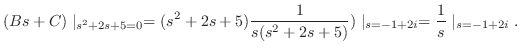
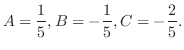
![$\displaystyle {\cal L}^{-1}[\frac{1}{s(s^2 + 2s +5)}]$](img1567.png) |
 |
![$\displaystyle {\cal L}^{-1}[\frac{1/5}{s}] -\frac{1}{5}\frac{s+2}{s^2+2s +5}$](img1568.png) |
|
 |
![$\displaystyle \frac{1}{5} -\frac{1}{5}{\cal L}^{-1}[\frac{s+1+1}{(s+1)^2 + 2^2}]$](img1569.png) |
||
 |
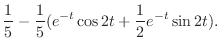 |
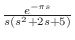 の逆変換は第2移動法則をつかって求める.第2移動法則より
の逆変換は第2移動法則をつかって求める.第2移動法則より
![$\displaystyle {\cal L}^{-1}[\frac{e^{-\pi s}}{s(s^2+2s+5)}] = u_{\pi}(t)f(t-\pi), $](img1572.png)
![$\displaystyle f(t) = {\cal L}^{-1}[\frac{1}{s(s^2 + 2s +5)}] = \frac{1}{5} -\frac{1}{5}(e^{-t}\cos{2t}+\frac{1}{2}e^{-t}\sin{2t}). $](img1573.png)
![$\displaystyle {\cal L}^{-1}[\frac{e^{-\pi s}}{s(s^2+2s+5)}] = u_{\pi}(t)f(t-\pi)$](img1574.png) |
|||
 |
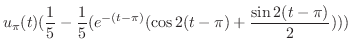 |
![$\displaystyle y(t) = {\cal L}^{-1}[Y(s)]$](img1576.png) |
 |
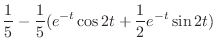 |
|
 |
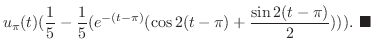 |
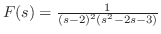 のとき
のとき
![${\cal L}^{-1}[F(s)]$](img1580.png) を求めよ.
を求めよ.
解
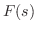 を部分分数分解を用いて展開すると
を部分分数分解を用いて展開すると
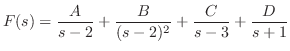
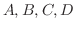 を求めると,
を求めると,