Next: 演習問題5.3.1 Up: ラプラス変換(The Laplace transformation) Previous: 演習問題5.2 目次 索引
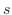 での積・
での積・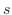 での商・そして移動に変わります.これらの性質と線形性によりラプラス変換は簡単に計算できるので応用範囲が広がり,便利な道具として発展してきました.
での商・そして移動に変わります.これらの性質と線形性によりラプラス変換は簡単に計算できるので応用範囲が広がり,便利な道具として発展してきました.
|
定理 5..2 (線形法則) 任意の定数
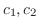 に対して, に対して,
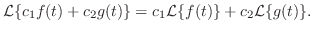
|
証明
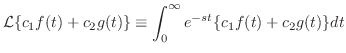
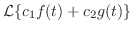 |
 |
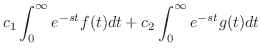 |
|
 |
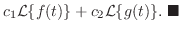 |
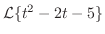 を求めよ.
を求めよ.
解
線形法則より
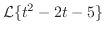 |
 |
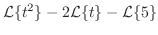 |
|
 |
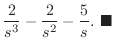 |
|
定理 5..3 (第1移動法則)
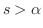 のとき のとき
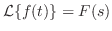 ならば, ならば,
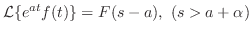
(注) |
証明
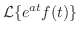 |
 |
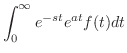 |
|
 |
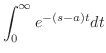 |
||
 |
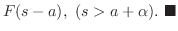 |
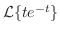 を求めよ.
を求めよ.
解
表5.1より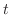 のラプラス変換は
のラプラス変換は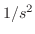 .よって第1移動法則より,
.よって第1移動法則より,
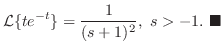
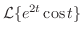 を求めよ.
を求めよ.
解
表5.1より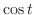 のラプラス変換は
のラプラス変換は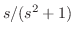 .よって第1移動法則より
.よって第1移動法則より
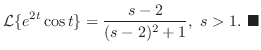
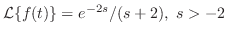 のとき,
のとき,
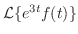 を求めよ.
を求めよ.
解
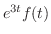 のラプラス変換は
のラプラス変換は のラプラス変換
のラプラス変換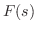 の
の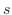 を
を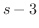 に置き換えることによって得られる.したがって
に置き換えることによって得られる.したがって
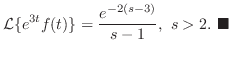
|
定理 5..4 (第2移動法則) 任意の正の数
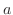 に対して に対して
|
証明
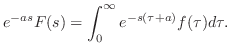
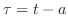 とおくと
とおくと
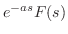 |
 |
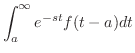 |
|
 |
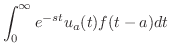 |
||
 |
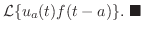 |
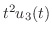 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
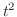 を
を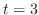 についてTaylor展開すると,
についてTaylor展開すると,
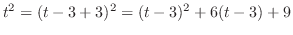
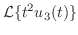 |
 |
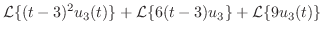 |
|
 |
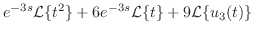 |
||
 |
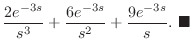 |
別解
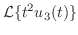 |
 |
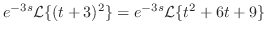 |
|
 |
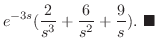 |
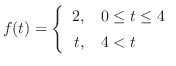 のラプラス変換を求めよ.
のラプラス変換を求めよ.
解
 を単位ステップ関数を用いて表わすと
を単位ステップ関数を用いて表わすと
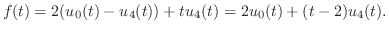
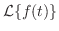 |
 |
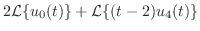 |
|
 |
 |